Question

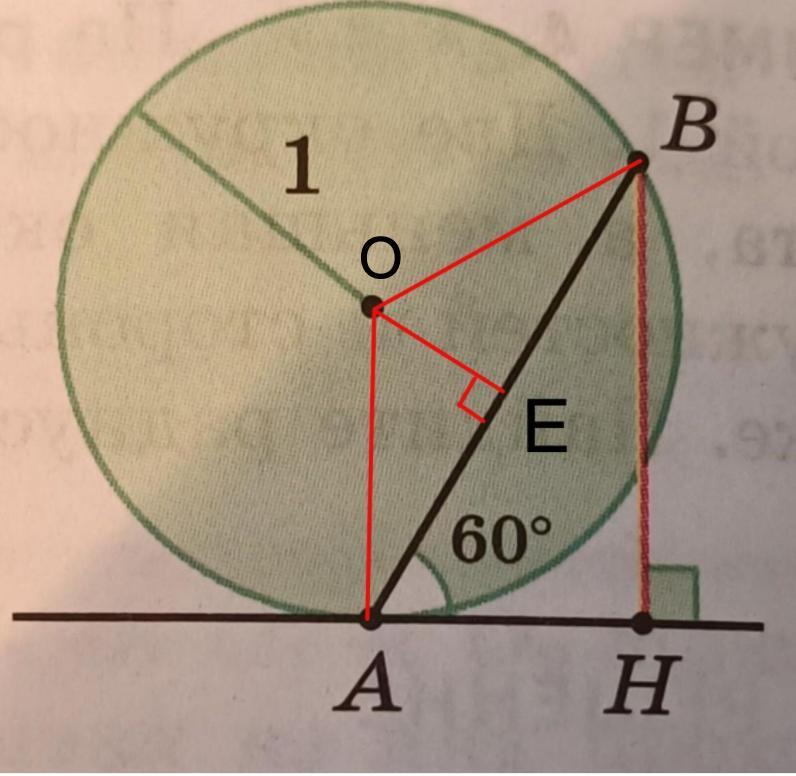
Прямая касается окружности радиуса 1 в точке А. Хорда АВ образует с касательной угол 60 градусов . Найдите длину перпендикуляра, опущенного из точки В на эту касательную.
Срочно!​

Answer 1

Ответ:

Длина перпендикуляра, опущенного из точки В на касательную равна 1,5 ед.

Объяснение:

Требуется найти длину перпендикуляра, опущенного из точки В на касательную.

Дано: Окр.О,R; R = 1.

АН - касательная;

АВ - хорда;

∠ВАН = 60°;

ВН ⊥ АН.

Найти: ВН.

Решение:

Дополнительное построение:

Соединим точку О с точками А и В.

ОЕ ⊥АВ.

1. ∠ВАН = 60°

• Угол между касательной и хордой равен половине дуги, заключенной внутри него.

⇒ ∪ АВ = 60° · 2 = 120°

2. Рассмотрим ΔАОВ.

• Центральный угол равен градусной мере дуги, на которую он опирается.

⇒ ∠АОВ = 120°

ОВ = ОА = R

⇒ ΔАОВ - равнобедренный.

• В равнобедренном треугольнике высота, проведенная к основанию, является медианой и биссектрисой.

⇒ ОЕ - высота, медиана, биссектриса.

⇒АЕ = ЕА; ∠АОЕ = ∠ЕОВ = 120° : 2 = 60°

3. Рассмотрим ΔАОЕ - прямоугольный.

• Сумма острых углов прямоугольного треугольника равна 90°.

⇒ ∠ОАЕ = 90° - 60° = 30°

• Катет, лежащий против угла в 30°, равен половине гипотенузы.

⇒  $\displaystyle OE = \frac{1}{2}\;OA=\frac{1}{2}$

По теореме Пифагора:

$\displaystyle AE = \sqrt{AO^2-OE^2}=\sqrt{1-\frac{1}{4} } =\frac{\sqrt{3} }{2}$

⇒ $\displaystyle AB = \sqrt{3}$

4. Рассмотрим ΔАВН - прямоугольный.

∠В = 90° - 60° = 30°

⇒ $\displaystyle AH=\frac{1}{2}\;AB = \frac{\sqrt{3} }{2}$

По теореме Пифагора:

$\displaystyle BH = \sqrt{AB^2-AH^2}=\sqrt{3-\frac{3}{4} }=\frac{3}{2}=1,5$

Длина перпендикуляра, опущенного из точки В на касательную равна 1,5 ед.