Question

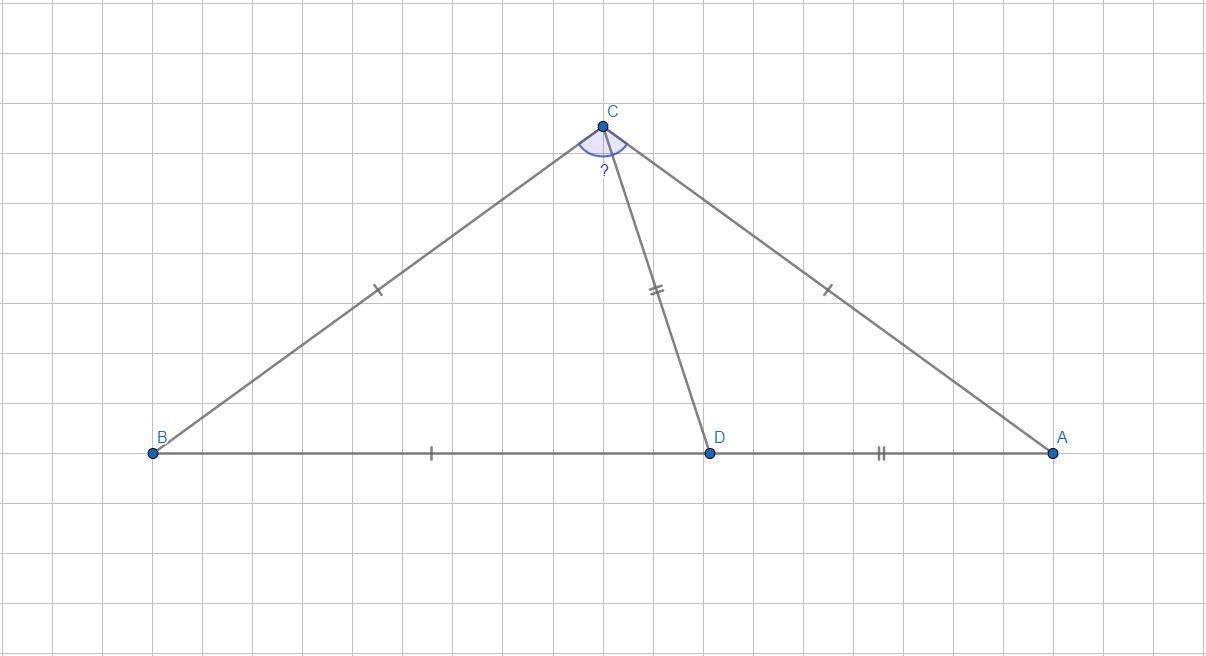
Дан равнобедренный треугольник ABC (AC = BC) и точка D на основании AB такая, что AD = CD и AC = BD. Найдите градусную меру ∠ ACB.​

Answer 1

Ответ:

• $\displaystyle \boldsymbol{\angle ACB}=\boldsymbol{108^\circ}$

Объяснение:

• В равнобедренном треугольнике углы при основании равны.

1. Т.к. ΔABC - равнобедренный по условию, то пусть ∠CAB=∠CBA=x.

ΔADC - равнобедренный, т.к. AD=CD по условию, тогда ∠CAD=∠ACD=x.

• Теорема о сумме углов треугольника: Сумма углов треугольника равна 180°.

2. Рассмотрим ΔDBC:

ΔDBC - равнобедренный, т.к. AC=BC=BD, тогда из т. о сумме углов треугольника: $\displaystyle \boldsymbol{\angle BCD}=\angle BDC=\frac{180^\circ-\angle CBD}{2} =\frac{180^\circ-x}{2} =\boldsymbol{90^\circ-\frac{x}{2}}$.

3. Рассмотрим ΔABC:

По т. о сумме углов треугольника:

$\displaystyle \angle CBA+\angle CAB+\angle ACB=180^\circ\\\angle CBA+\angle CAB+\angle BCD+\angle ACD=180^\circ\\x+x+90^\circ-\frac{x}{2} +x=180^\circ\\2,5\cdot x=90^\circ\\x =36^\circ$

4. Тогда $\displaystyle \boldsymbol{\angle ACB}=\angle BCD+\angle ACD=90^\circ-\frac{x}{2} +x=90^\circ+\frac{36^\circ}{2} =\boldsymbol{108^\circ}$.