Заполните пропуски в тексте так, чтобы получилось правильное решение.
Задача. На сторонах параллелограмма внешним образом построены квадраты. Докажите, что их центры образуют квадрат, причём центр параллелограмма является центром этого квадрата.
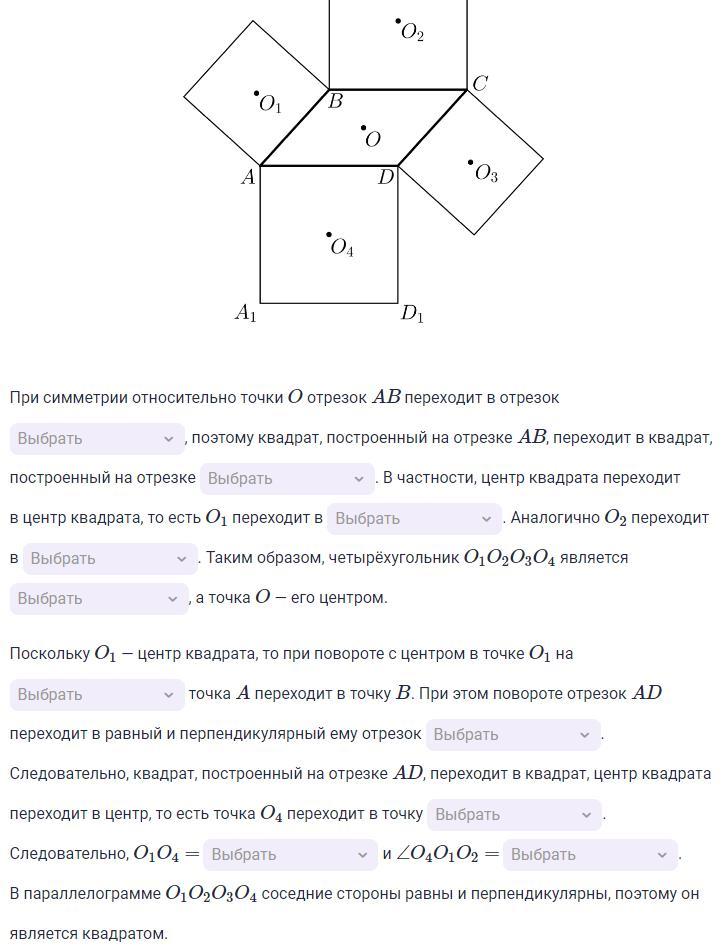
Решение. Введём обозначения, как показано на рисунке.
Ответы
При симметрии относительно точки O отрезок AB переходит в отрезок CD, поэтому квадрат, построенный на отрезке AB переходит в квадрат, построенный на отрезке CD. В частности, центр квадрата переходит в центр квадрата, то есть O1 переходит в O3. Аналогично O2 переходит в O4. Таким образом четырехугольник O1O2O3O4 является параллелограммом, а точка O - его центром.
Поскольку O1 - центр квадрата, то при повороте с центром в точке O1 на 90° против часовой стрелки точка A переходит в точку B. При этом повороте отрезок AD переходит в равный и перпендикулярный ему отрезок BB1. Следовательно, квадрат, построенный на отрезке AD, переходит в квадрат, центр квадрата переходит в центр, то есть точка O4 переходит в точку O2.
Следовательно, O1O4=O1O2 и ∠O4O1O2=90°.
В параллелограмме O1O2O3O4 соседние стороны равны и перпендикулярны, поэтому он является квадратом.