Question

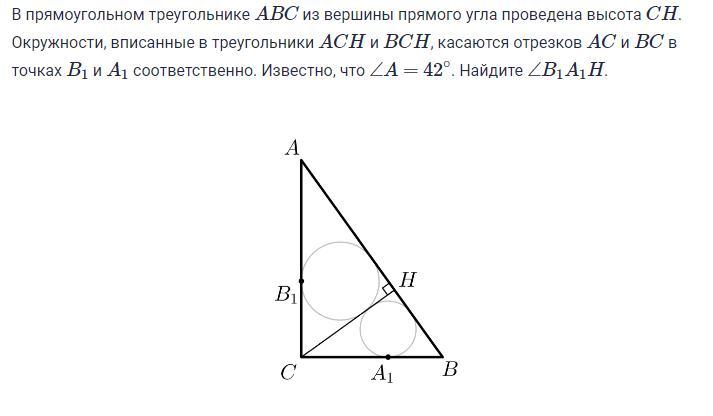
В прямоугольном треугольнике ABC из вершины прямого угла проведена высота CH. Окружности, вписанные в треугольники ACH и BCH, касаются отрезков AC и BC в точках B1 и A1 соответственно. Известно, что ∠A=42∘. Найдите ∠B1A1H.

Answer 1

△ACH ~ △ABC ~ △CBH (по углам)

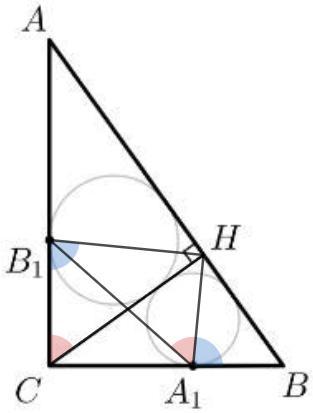
Треугольники ACH и CBH подобны. HB1 и HA1 - соответствующие отрезки => ∠HB1C=∠HA1B

В четырехугольнике CB1HA1 внешний угол равен противолежащему внутреннему => четырехугольник вписанный.

Тогда ∠B1A1H =∠B1CH (вписанные углы) =∠ACH =90°-∠A =48°