Question

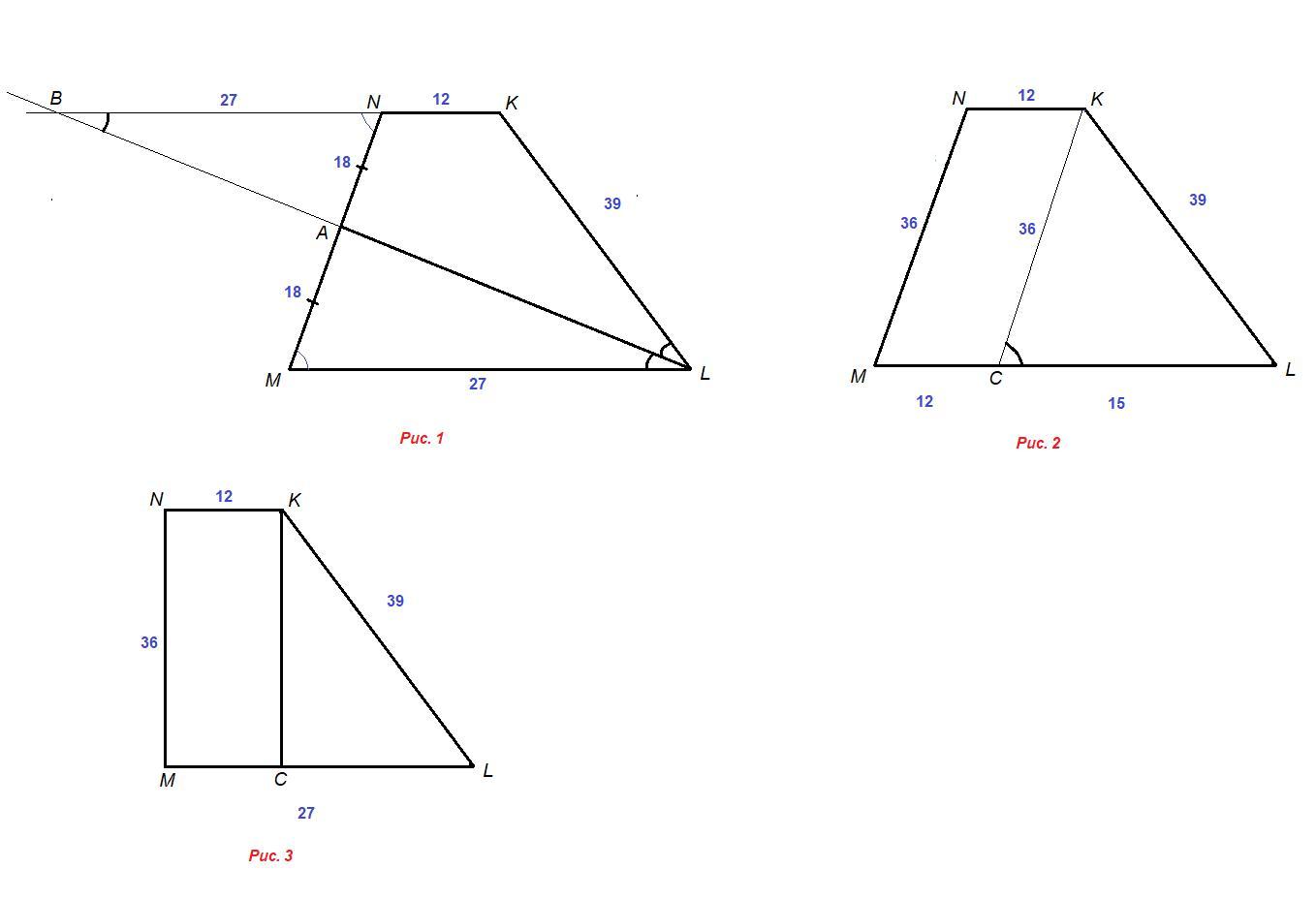
Дана трапеция mnkl . Ее верхнее основание nk = 12 , а боковые стороны mn и kl равны соответственно 36 и 39 . Биссектриса угла mlk проходит через середину стороны mn . Найдите площадь трапеции .

Answer 1

Ответ:

702 кв. ед.

Объяснение:

Чтобы найти площадь трапеции, надо знать длины оснований и высоту.

Рисунок 1.

Продлим биссектрису LA до пересечения с прямой NK (точка В).

ΔMAL = ΔNAB по стороне и двум прилежащим к ней углам:

• МА = AN, так как А - середина MN,
• ∠MAL = ∠NAB как вертикальные,
• ∠AML = ∠ANB как накрест лежащие при пересечении параллельных прямых ML и NK секущей MN.

Тогда BN = ML.

∠MLA = ∠KLA, так как LA биссектриса,

∠MLA = ∠NBA как накрест лежащие при пересечении параллельных прямых ML и NK секущей LB, значит

∠KLA = ∠NBA и значит ΔKBL равнобедренный с основанием LB, ⇒

КВ = KL = 39

BN = KB - NK = 39 - 12 = 27

ML = BN = 27

Рисунок 2.

Проведем КС║MN, а так как и NK║MC, то MNKC - параллелограмм,

МС = KN = 12

KC = MN = 36

CL = ML - MC = 27 - 12 = 15

Рассмотрим треугольник CKL:

по теореме косинусов

KL² = KC² + CL² - 2 · KC · CL · cos∠C

39² = 36² + 15² - 2 · 36 · 15 · cos∠C

1521 = 1296 + 225 - 1080 · cos∠C

1080 · cos∠C = 0   ⇒

∠C = 90°

То есть КС⊥ML, значит трапеция прямоугольная и MN = 36 - ее высота (рисунок 3)

Площадь трапеции:

$S=\dfrac{ML+KN}{2}\cdot MN$

$\boldsymbol{S}=\dfrac{27+12}{2}\cdot 36=39\cdot 18\boldsymbol{=702}$