Question

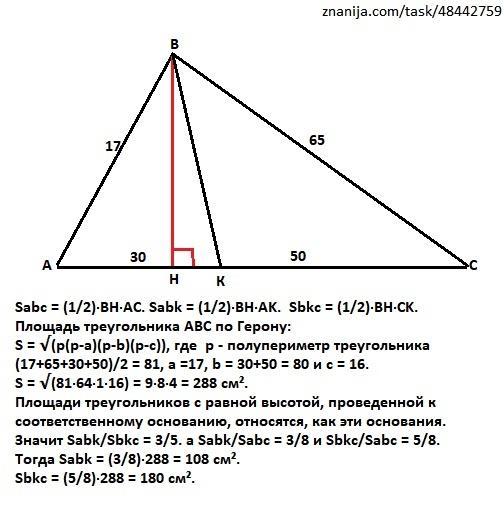
Дан треугольник ABC. На стороне AC отмечена точка K так, что AK=30см, KC=50см. Найдите площадь треугольников ABK и BKC, если AB=17см, BC=65см. Пожалуйста, все распишите !!​

Answer 1

Ответ:

Sabk = 108 см².

Sbkc = 180 см².

Объяснение:

Площадь треугольника АВС по Герону:

S = √(p(p-a)(p-b)(p-c)), где  p - полупериметр треугольника (17+65+30+50)/2 = 81, а =17, b = 30+50 = 80 и с = 16.

S = √(81·64·1·16) = 9·8·4 = 288 см².

Площади треугольников с равной высотой, проведенной к соответственному основанию, относятся, как эти основания.

Значит Sabk/Sbkc = 3/5. а Sabk/Sabc = 3/8 и Sbkc/Sabc = 5/8.

Тогда Sabk = (3/8)·288 = 108 см².

Sbkc = (5/8)·288 = 180 см².