Question

СРОЧНО СДЕЛАЙТЕ ПОЛНОСТЬЮ ВСЕ ЗАДАНИЯ

Answer 1

Ответ:          

Функция возрастает на промежутках, где её производная неотрицательна, и убывает на тех промежутках, где производная неположительна.

Так как задан график производной, то надо определить, где  $f'(x)\geq 0$ и  где  $f'(x)\leq 0$  .

Функция возрастает при   $x\in (-7\, ;-5,5\, ]\ \ ,\ \ x\in [-2,5\, ;\ 4\ )$  .

Функция убывает при   $x\in [-5,5\, ;-2,5\, ]$  .

Answer 2

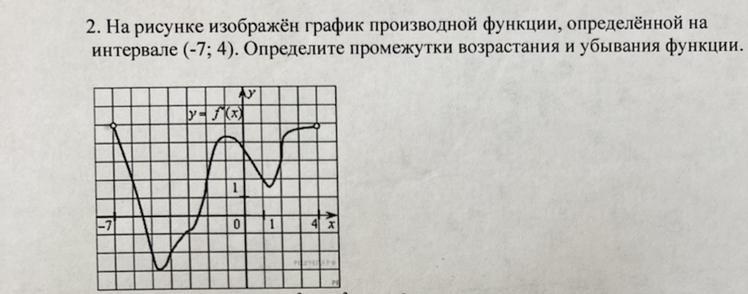
поскольку дан график производной функции, то смотрим, где он ниже оси ох, при таких значениях х функция убывает, поскольку по графику видно, что функция непрерывна в точках пересечения с осью ох, то и точки пересечения можно включать в промежуток убывания, те же значения х, при которых график находится выше оси ох или пересекает эту ось - это промежутки возрастания.

точки х=-7 и х=4 не включаются в ответы по причине того, что они выколоты и не входят в область определения функции.

поэтому функция убывает при х∈[-5.5; -2.5]

и возрастает при х∈(-7; -5.5] и при х∈[-2.5; 4)

Если речь идет о строгом убывании и возрастании, тогда уместен ответ: функция убывает при х∈(-5.5; -2.5) и возрастает при х∈(-7; -5.5) и при х∈(-2.5; 4)

Замечу, что если промежутков возрастания или убывания несколько, то слово или, а также значок объединения ∪ здесь неуместны, нужно ответ подавать либо через запятую, либо с союзом и.