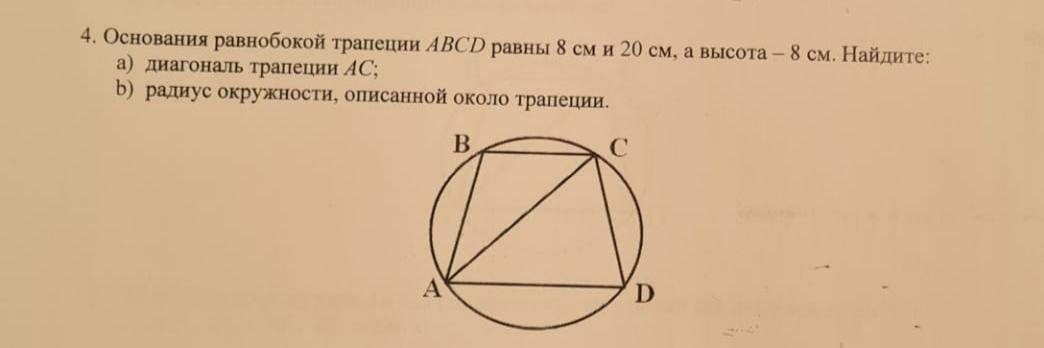
основания равнобедренной трапеции ABCD равны 8 см и 20 см а высота -8см найдите а) диагональ трапеции AC б) радиус окружности описаной около трапеции
Ответы
Ответ:
1) AC = 2√65 см; 2) R = 5√65/4 см.
Объяснение:
Дана равнобочная трапеция.
Основания a = 8 см, b = 20 см, высота h = 8 см.
Найти: а) диагональ AC; б) радиус описанной окружности R.
Решение:
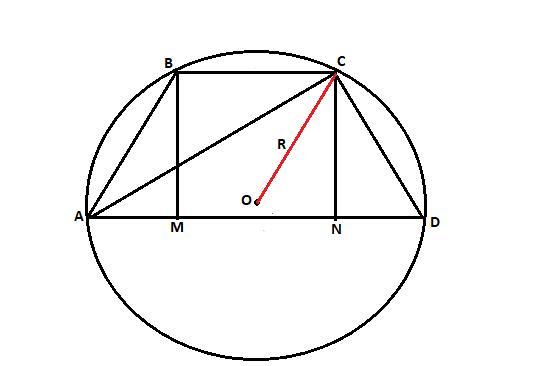
Смотрите рисунок.
AD = 20 см, BC = MN = 8 см, BM = CN = 8 см, AM = DN, OC = R.
а) Мы видим, что:
AD = AM + MN + ND
20 = 2*ND + 8
ND = (20 - 8)/2 = 12/2 = 6 см
Из теоремы Пифагора для треугольника ACN:
AC^2 = AN^2 + CN^2
AC^2 = (AM + MN)^2 + CN^2 = (6 + 8)^2 + 8^2 = 196 + 64 = 260
AC = √260 = 2√65 см.
2) Заметим, что окружность, описанная около трапеции, также описана около треугольника ACD.
Из прямоугольного треугольника CDN получаем:
CN = 8 см, ND = 6 см
CD^2 = CN^2 + ND^2 = 8^2 + 6^2 = 64 + 36 = 100
CD = 10 см
sin D = CN/CD = 8/10 = 0,8
Из теоремы синусов для треугольника ACD:
AC/sin D = 2R
R = AC/(2sin D) = 2√65/(2*0,8) = √65/0,8 = √65 : (4/5) = 5√65/4