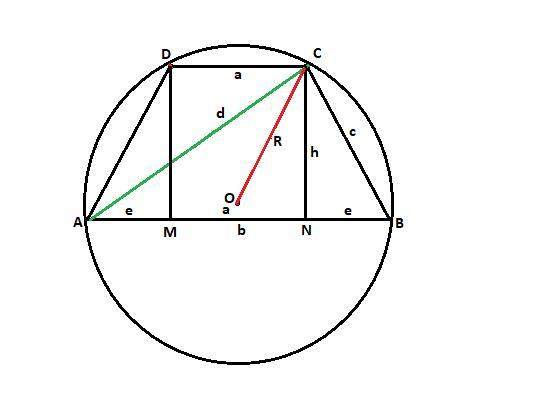
Задание 4. Основания равнобокой трапеции ABCD равны 8 см и 20 см, а высота – 8 см. Найдите: а) диагональ трапеции Ад; б)радиус окружности, описанной около трапеции, 4 балла)
Ответы
Ответ:
1) AC = √260 см; 2) R = 5√260/8 см.
Объяснение:
Дана равнобочная трапеция.
Основания a = 8 см, b = 20 см, высота h = 8 см.
Найти: а) диагональ AC; б) радиус описанной окружности R.
Решение:
Смотрите рисунок.
AB = b = 20 см, CD = MN = a = 8 см, DM = CN = h = 8 см, BC = c, AC = d, AM = BN = e, OC = R.
а) Тут явно опечатка в задании. AD - это сторона трапеции.
А найти требуется диагональ AC. Мы видим, что:
AB = AM + MN + NB
b = e + a + e
20 = 2e + 8
e = (20 - 8)/2 = 12/2 = 6 см
Из теоремы Пифагора для треугольника ACN:
AC^2 = AN^2 + CN^2
d^2 = (e + a)^2 + h^2 = (6 + 8)^2 + 8^2 = 196 + 64 = 260
AC = d = √260 см.
2) Заметим, что окружность, описанная около трапеции, также описана около треугольника ABC. Найдем её радиус по формуле:
R = bdc/(4*S(ABC))
Из теоремы Пифагора для треугольника BCN:
c^2 = h^2 + e^2 = 8^2 + 6^2 = 64 + 36 = 100
c = 10 см
Площадь треугольника ABC:
S(ABC) = b*h/2 = 20*8/2 = 80 см^2
Радиус описанной окружности:
OC = R = 20*√260*10/(4*80) = 5√260/8 см