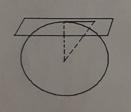
Расстояние от точки касательной плоскости до центра шара равно 20 см, а расстояние от нее до точки касания - 16 см. Найдите объем шара.
Ответы
Зная радиус сферы, нужно найти расстояние от центра до плоскости. Для этого достаточно найти радиус окружности, полученной в сечении сферы плоскостью. Тогда из прямоугольного треугольника онк
0-центр сферы, н - центр окружности сечения, к-точка на этой окружности) мы сможем найти искомое расстояние.
Найдем радиус окружности сечения. Она
является вписанной для треугольника АВС
Воспользуемся формулой: S = pr.
r = P
AB+BC+CA 2 13+14+15 2 p = полупериметр. = 21 (см) -
Найдем площадь треугольника по формуле Герона:
S = √p(p-AB) (p - BC)(p-CA) | = √21-8 -7 - 6 = 84 (см²)
Соответственно: r === P 84 21 = 4 (см).
Найдем расстояние от центра сферы до плоскости.Искомое расстояние - это катет треугольника окн с гипотенузой 5 и другим катетом 4. Тогда легко показать, что ОН = 3 см
Ответ: расстояние от центра сферы до
плоскости АВС равно 3 см.Искомое расстояние - это катет треугольника окн с гипотенузой 5 и другим катетом 4. Тогда легко показать, что ОН = 3 см
Ответ: расстояние от центра сферы до
плоскости АВС равно 3 см.