Предмет: Геометрия, автор: linavasilenko5365

Ландшафтный архитектор рассматривает по карте земельный участок, который имеет форму параллелограмма. На чертеже стороны земельного участка равны 30 см и 25 см, а угол между этими сторонами составляет 75°. Архитектор планирует построить забор вдоль большей диагонали. Определи, какова будет длина забора, если масштаб карты 1:1 440. Ответ округли до целого.

Ответы

Автор ответа: ariana7561

Ответ:

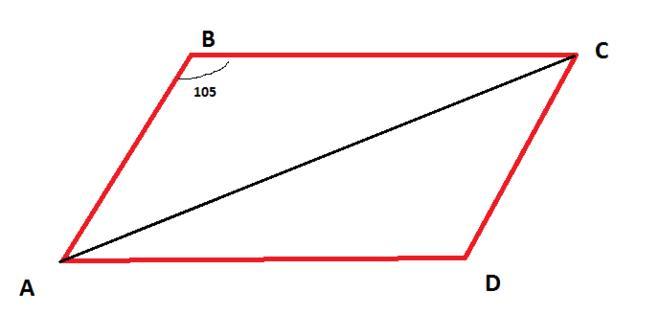
Обозначим параллелограмм на чертеже участка через ABCD и попробуем найти его диагональ. Очевидно, что большая диагональ - это АС.

Сначала найдем угол В, используя свойство параллелограмма (сумма смежных углов параллелограмма равна 180 градусов). Угол В равен 180-75=105 градусов. Теперь можно воспользоваться теоремой косинусов, чтобы найти третью сторону треугольника АВС (большую диагональ АС). AC^2=AB^2+BC^2-2*AB*BC*cosB = 30^2+25^2-2*30*25*cos105=900+625+1500*0,26=1913,23. Извлекаем квадратный корень и получим АС = V1913,23 = 43,74 см. Теперь можно перевести эту длину в реальный масштаб.

43,74*1440=62986 см или около 630 метров.

Ответ: 630 м.

Приложения: