Question

В фото задание
Плззз​

Answer 1

Ответ:

Наименьшее возможное значение числа АТВ равно 512.

Пошаговое объяснение:

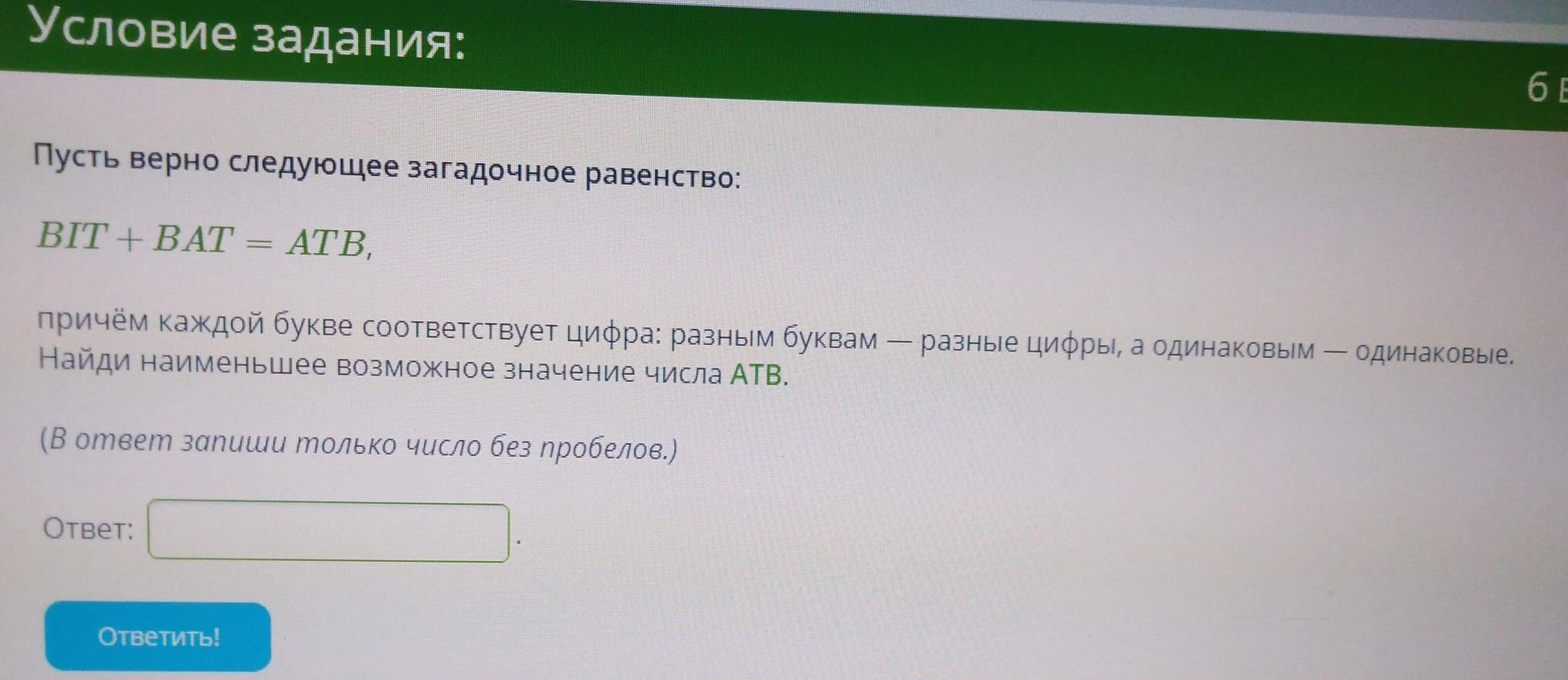
Найти наименьшее возможное значение числа АТВ.

Пусть верно следующее загадочное равенство:

BIT + BAT = ATB

Одинаковым буквам соответствуют одинаковые цифры, разным буквам - разные цифры.

Запишем в столбик данное равенство:

$\displaystyle \begin{equation*} \begin{} BIT\\ + \\ BAT \\--- \\ ATB \end{cases}\end{equation*}$

Так как нам нужно минимальное значение, то примем В за 1. Тогда и последняя цифра в сумме должна быть 1. Но эта цифра может быть только четной, так как складываются два одинаковых числа.

Тогда примем В за 2. Последняя цифра в сумме будет 2.

$\displaystyle \begin{equation*} \begin{} 2IT\\ + \\ 2AT \\--- \\ AT2 \end{cases}\end{equation*}$

Т может быть или 1 (1 + 1 = 2) или 6 (6 + 6 = 12)

Подставим вместо Т цифру 1.

Получим:

$\displaystyle \begin{equation*} \begin{} 2I1\\ + \\ 2A1 \\--- \\ A12 \end{cases}\end{equation*}$

I и А в сумме должны дать число, которое оканчивается на 1. Эта сумма равна 11. Значит А будет равно 2 + 2 + 1 = 5, а I соответственно 6.

Получим:

$\displaystyle \begin{equation*} \begin{} 261\\ + \\ 251 \\--- \\ 512 \end{cases}\end{equation*}$

Все получилось.

Но проверим еще Т = 6.

$\displaystyle \begin{equation*} \begin{} 2I6\\ + \\ 2A6 \\--- \\ A62 \end{cases}\end{equation*}$

Сумма I и А должна оканчиваться на 6. С другой стороны, первая цифра А в сумме может быть или 4 или 5.

Если А = 4, то I = 2, но у нас есть В = 2.

Если А = 5, то сумма I и А должна быть равна 16. Что тоже невозможно.

Следовательно, первый вариант верный.

Наименьшее возможное значение числа АТВ равно 512.