Question

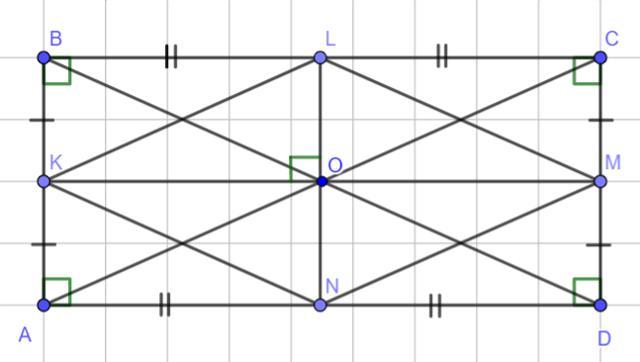
решение записывать подробно! Задание 1. Задан прямоугольник ABCD. K – середина AB, L – середина BC, M – середина CD, N – середина AD. а) Докажите, что KLMN – ромб (14 баллов). б) Найдите периметр и площадь KLMN, если AB = 18 см, BC = 24 см (16 баллов).

Answer 1

а)

KL — средняя линия треугольника ABC (потому что соединяет середины его сторон), и, по свойству средней линии, $\displaystyle KL = \frac{1}{2} AC$.

LM — средняя линия треугольника BCD, и поэтому $\displaystyle LM = \frac{1}{2} BD$.

MN — средняя линия треугольника CDA, и поэтому $\displaystyle MN = \frac{1}{2} AC$ .

NK — средняя линия треугольника DAB, и поэтому $\displaystyle NK = \frac{1}{2} BD$.

По свойству прямоугольника, его диагонали равны: AC = BD.

Это значит, что KL = LM = MN = NK.

Четырехугольник, у которого все стороны равны, является ромбом.

Отсюда, KLMN – ромб. Что и требовалось доказать.

б)

Поскольку K — середина стороны AB, то KB = AB : 2 = 18 : 2 = 9 (см).

Поскольку L — середина BC, то BL = 24 : 2 = 12 (см).

ΔKBL — прямоугольный (∠B = 90°, потому что это угол прямоугольника).

По теореме Пифагора:

KL² = KB² + BL² = 9² + 12² = 81 + 144 = 225

Отсюда, KL = √225 = 15 (см).

Значит, стороны ромба равны 15 см. Найдем периметр:

$P_{KLMN} = 4 \cdot 15 = 60$ (см).

Теперь найдем площадь.

Диагонали ромба перпендикулярны друг другу (LN ⊥ KM). Поэтому BLOK, LCMO, KONA и OMDN являются прямоугольниками.

Это значит, что диагональ LN параллельна и равна сторонам AB и CD, а диагональ KM параллельна и равна сторонам BC и AD.

LN = AB = 18 см, KM = BC = 24 см.

Площадь ромба равна половине произведения диагоналей, поэтому:

$\displaystyle S_{KLMN} =\frac{LN\cdot KM}{2}=\frac{18\cdot 24}{2}= 216$ (см²).

Ответ: P = 60 см, S = 216 см².