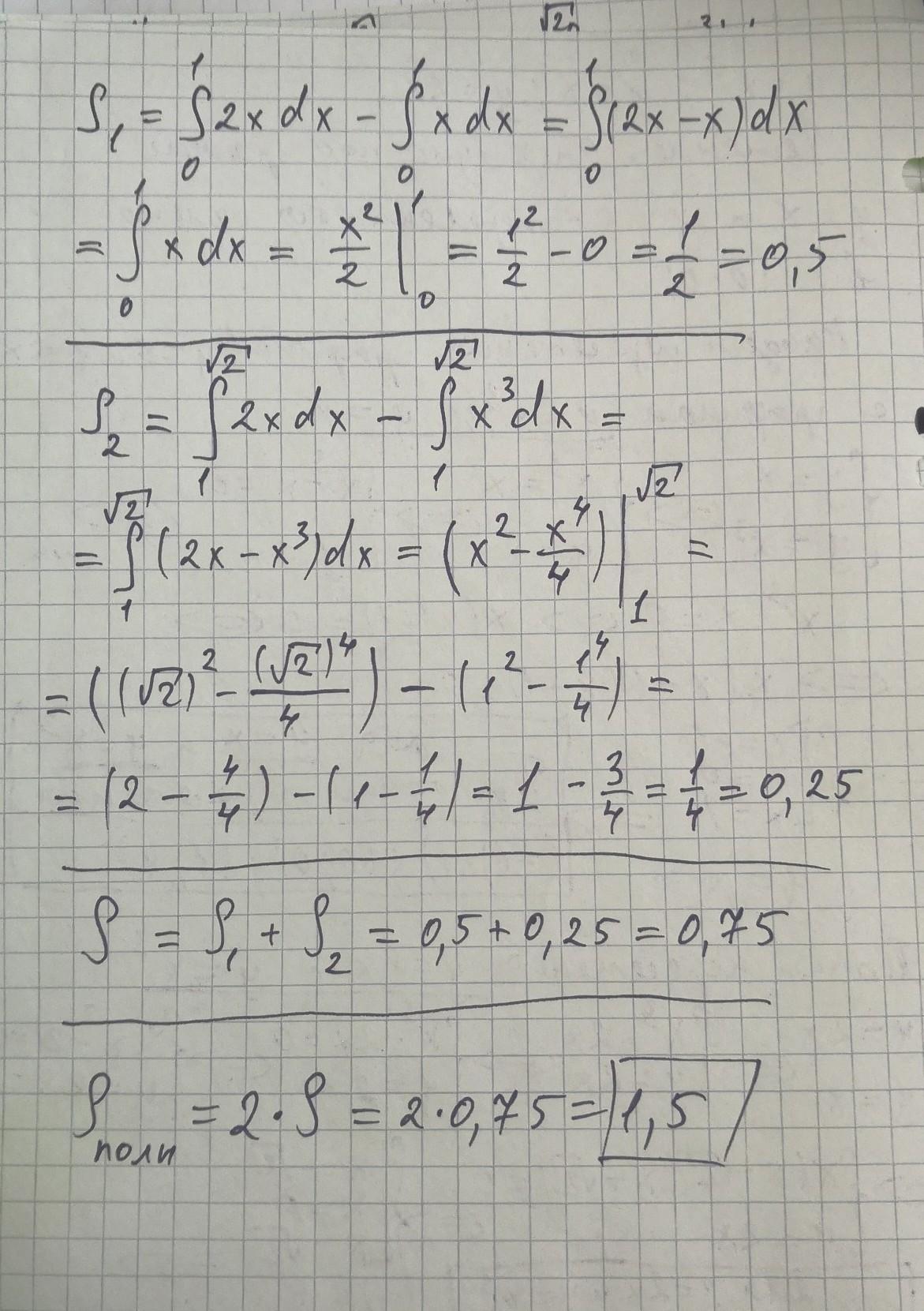Question

Найти площадь фигуры ограниченную линиями y=x^{3} и y=2x; y=x

Answer 1

Ответ:

$S_{obw} = 1.5$

Пошаговое объяснение:

1. Очевидно, что прямые

у = х и у = 2х

пересекаются только в т. (0; 0).

Найдем пересечения прямых с графиком ф-ии

у = х³

Для этого - составим и решим системы (см. на рис.)

Для у = х и у = х³ это 3 точки

$(-1;-1),\; (0;0),\;(1;1)$

Для у = 2х и у = х³ это 3 точки

$(- \sqrt{2} ; \,-2 \sqrt{2}),\; (0; \, 0),\;( \sqrt{2} ; \,2 \sqrt{2} )$

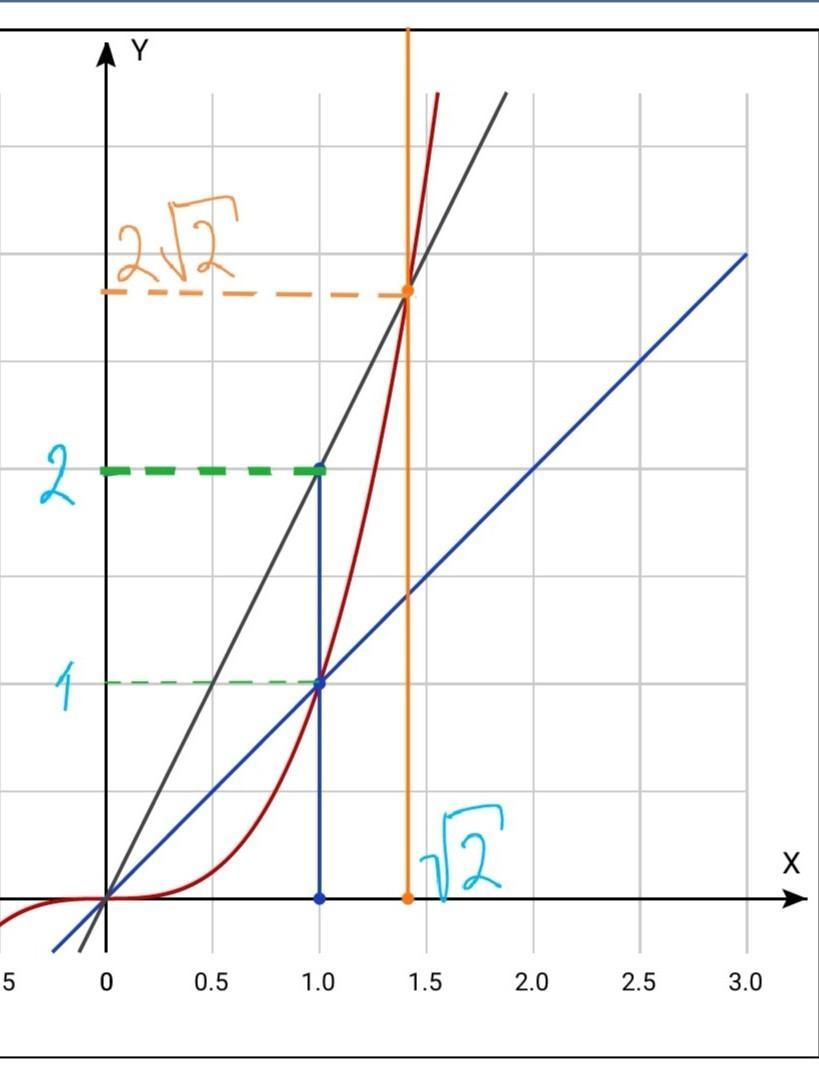
2. Построим графики функций (см. рис.)

у = х;

у = х; у = 2х

у = х; у = 2ху = х³

(Примечание: Т.к. искомая фигура симметрична относительно (0;0), мы рассмотрим только половину искомой фигуры, расположенную в I четверти. Соответственно, полную площадь вычислим, удвоив полученный результат)

3. Искомую площадь удобнее искать, разбив на две части S1 и S2:

------------------------------------

Первая часть S1 (на промежутке [0; 1]) будет равна:

площадь ∆-ка под у = 2х на промежутке [0; 1]

минус

площадь ∆-ка под у = х на промежутке [0; 1]

------------------------------------

Вторая часть S2 (на промежутке [1; √2]) равна:

площадь ∆-ка под у = 2х на промежутке [1; √2]

]минус

площадь трапеции под у = х³ на промежутке [1; √2]

Нахождение S1, S2 производим путем вычисления определенных интегралов (см. рис.)

Получаем:

$S_1 = 0.5; \: \: \: \: S_2 = 0.25;$

В сумме это будет

$S = S_1 +S_2 = 0.75;$

А полная площадь фигуры (с учетом симметричной части в III четверти)

$S_{obw}=2\cdot 0.75 = 1.5$