Предмет: Геометрия,
автор: sowv
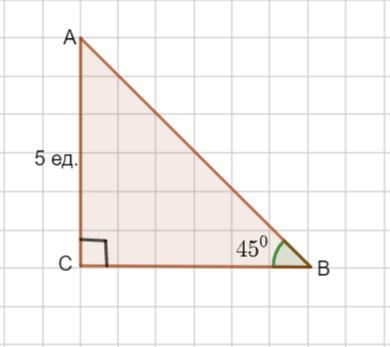
В прямоугольном треугольнике АВС (угол C-прямой) угол B=45°. AC=5. Найти: СВ. АВ.
Ответы
Автор ответа:
0
Ответ:
СВ = 5 ед.; AB =5√2 ед.
Объяснение:
Пусть дан Δ АВС - прямоугольный , ∠ С=90°, ∠В =45 °, АС= 5 ед.
Найдем СВ и АВ.
Сумма острых углов прямоугольного треугольника равна 90°.
Тогда ∠ А= 90 °- 45° = 45°.
Если в треугольнике два угла раны, то он равнобедренный и
АС= СВ = 5 ед.
Найдем гипотенузу АВ по теореме Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
AB =5√2 ед.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: аля15678
Предмет: Английский язык,
автор: dskyratova522
Предмет: Қазақ тiлi,
автор: mogilko88
Предмет: Русский язык,
автор: kseniiabudushchaia
Предмет: История,
автор: kokovina2912