Question

ПОМОГИТЕ ЗАДАЧА ТЯЖЁЛАЯ
Условие задания:

Квадрат, сторона которого составляет 24 см, повернули на плоскости по часовой стрелке так, что одна из его
вершин осталась на месте. Угол, на который повернули квадрат, составил 75°. Какова наименьшая из длин
следов, оставленных другими вершинами квадрата при повороте? Результат округли до сотых.
(Используйте =3,14. В ответ запиши только число без пробелов.)
Ответ:

Answer 1

Ответ:

Наименьшая из длин следов, оставленных другими вершинами квадрата при повороте равна 31,4 см.

Пошаговое объяснение:

Определить, какова наименьшая из длин следов, оставленных другими вершинами квадрата при повороте квадрата по часовой стрелке на угол 75°.

Дано: ABCD - квадрат;

α = 75° - угол поворота.

АВ = 24 см.

Найти: наименьшую из длин следов.

Решение:

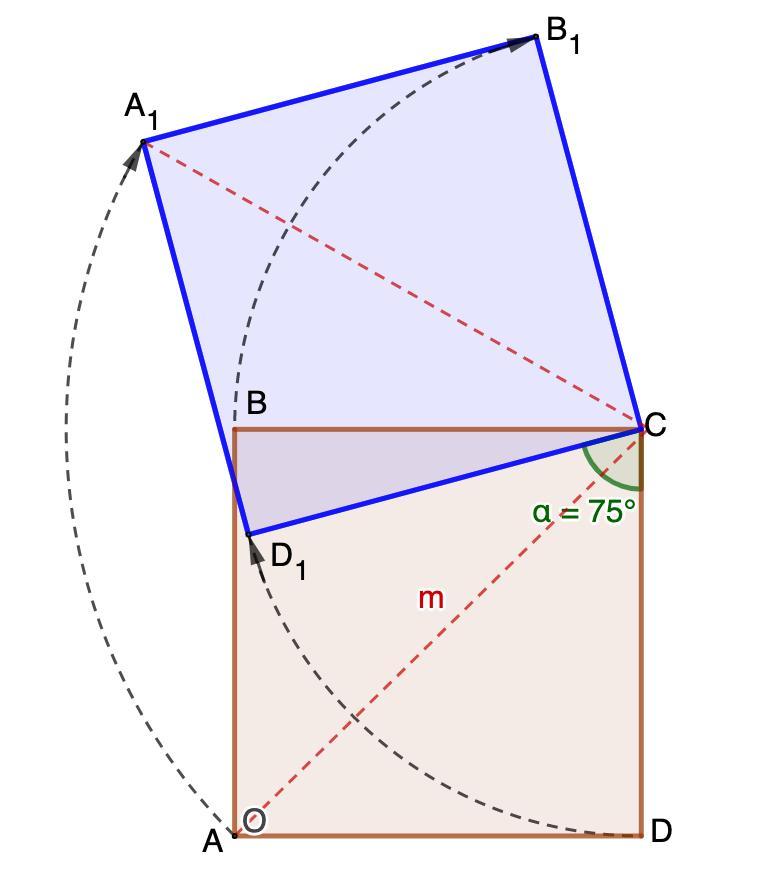
Будем поворачивать квадрат вокруг вершины С против часовой стрелки на угол 75°.

Точка С остается на месте, а точки A, B, и D отображаются в точки A₁, B₁, и D₁ так что CD = CD₁; CA = CA₁; CB = CB₁ и ∠DCD₁ = ∠ACA₁ = ∠BCB₁ = α = 75°.

Длина дуги равна:

$\displaystyle \boxed { l=\frac{\pi r}{180^0} \cdot{\alpha }}$

Длина дуги DD₁ будет равна длине дуги ВВ₁, так как у них равные радиусы 24 см и равные углы α = 75°.

Очевидно, что длина дуги АА₁ больше, так как ее радиус больше.

Поэтому найдем длину наименьшего следа, то есть длину дуги DD₁.

$\displaystyle \smile {DD_1}=\frac{\pi \cdot24}{180^0} \cdot{75^0}=3,14\cdot10 = 31,4 \;_{(CM)}$

Наименьшая из длин следов, оставленных другими вершинами квадрата при повороте равна 31,4 см.