Question

Задание 4.

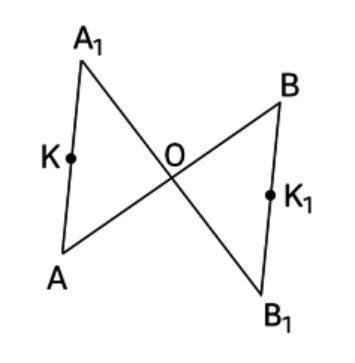
Отрезки AB и A1B1 имеют общую середину О. Докажите, что:

а) отрезки АA1 и BB1 равны (10 баллов);

б) точки K и K1 – середины отрезков A1А и B1B соответственно лежат на одной прямой, проходящей через точку О (15 баллов).

Примечание: для доказательства воспользуйтесь свойством угла KOK1.

Answer 1

Ответ:

а) ΔАА₁О = ΔВВ₁О по двум сторонам и углу между ними, так как

• АО = ОА₁ по условию,
• ВО = ОВ₁ по условию,
• ∠АОА₁ = ∠ВОВ₁ как вертикальные.

В равных треугольниках против равных углов лежат равные стороны, значит

АА₁ = ВВ₁.

б) Из равенства треугольников АА₁О и ВВ₁О следует, что

∠А = ∠В и ∠А₁ = ∠В₁.

Тогда ΔАКО = ΔВК₁О по двум сторонам и углу между ними:

• АК = ВК₁ как половины равных отрезков,
• АО = ОВ по условию,
• ∠А = ∠В (доказано выше).

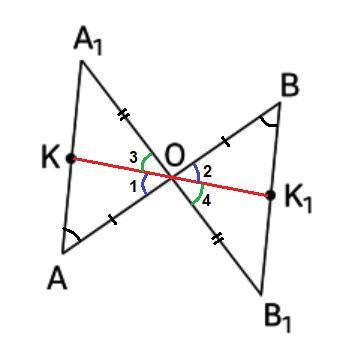
Значит, ∠1 = ∠2.

ΔА₁КО = ΔВ₁К₁О по двум сторонам и углу между ними:

• А₁К = В₁К₁ как половины равных отрезков,
• А₁О = ОВ₁ по условию,
• ∠А₁ = ∠В₁ (доказано выше).

Значит, ∠3 = ∠4.

Итак, ∠КОК₁ = ∠1 + ∠АОВ₁ + ∠4 (нижняя часть плоскости)

и ∠КОК₁ = ∠3 + ∠А₁ОВ + ∠2 (верхняя часть плоскости)

Так как ∠АОВ₁ = ∠А₁ОВ как вертикальные, то ∠КОК₁ = 180°, развернутый. Следовательно, точки К, К₁ и О лежат на одной прямой.