Предмет: Алгебра,
автор: svetlanabojko651
((sin a)/(1 + cos alpha) + (sin alpha)/(1 - cos alpha)) * sin 2alpha underline
Ответы
Автор ответа:
0
Ответ:
Объяснение:
Приложения:
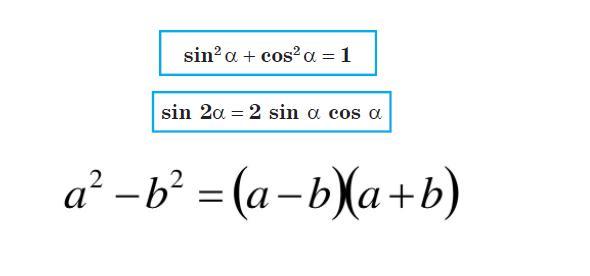
Похожие вопросы
Предмет: Русский язык,
автор: орхан2005
Предмет: Русский язык,
автор: egorkazakov
Предмет: Русский язык,
автор: marinaoskar
Предмет: Литература,
автор: davron199
Предмет: Русский язык,
автор: Аноним