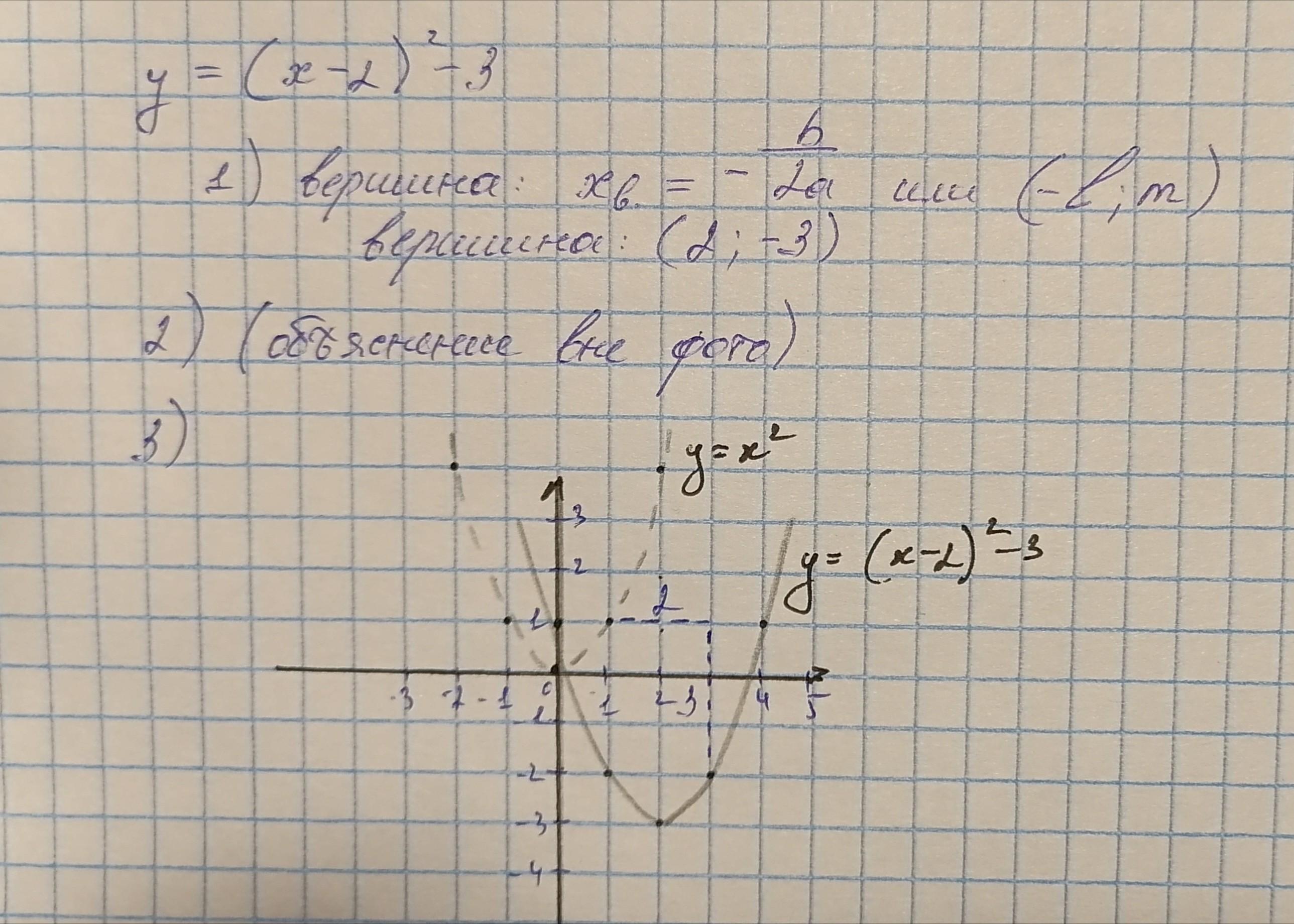Дана функция:y=(x-2)²-3
А)определите координаты вершины пораболы
Б)как построить график этой функции с помощью преобразований графика функции y=x²?
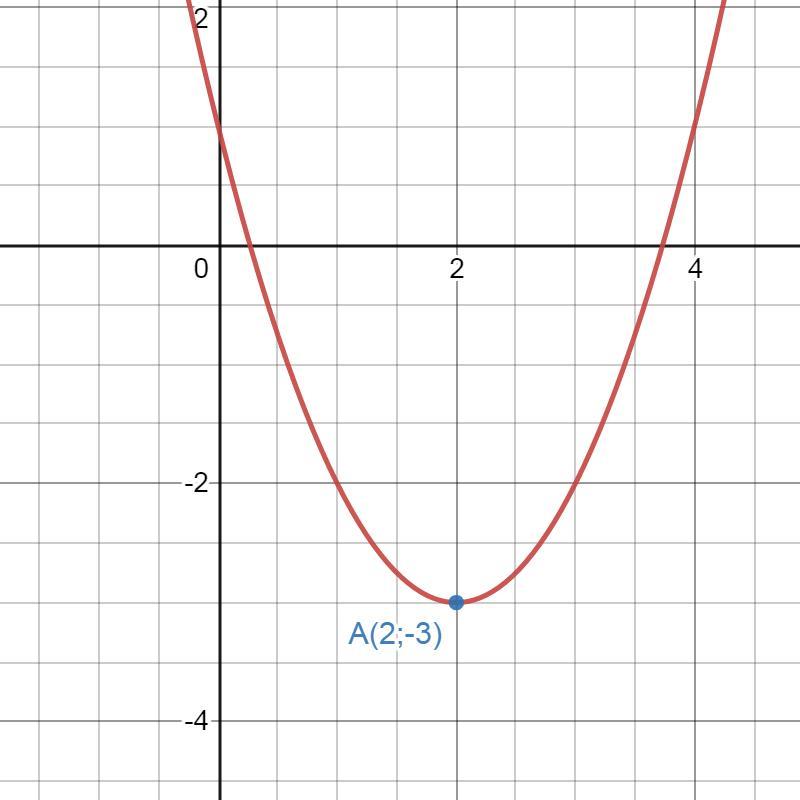
В)постройте график
СРОЧНО СРОЧНО
Ответы
Объяснение:
Б) Это график функции у=х², смещённый: вправо на две единицы относительно оси ОХ и вниз на три единицы относительно оси ОУ.
А) у=(х-2)²-3=х²-4х+4-3=х²-4х+1.
Хa=-4/(-2*1)=-4/-2=2.
Уa=(2-2)²-3=(0)²-3=-3 ⇒ A(2;-3).
1) Вершину можно определить двумя формулами, смотря как записана функция. В данном случае формула функции имеет вид f(x) = a(x+l)²+m. Формулу самой вершины для этого случая я указала на фото.
2) В данной записи y=(x-2)²-3 мы подразумеваем у=a(x+l)²+m, где a=1, l=-2, m=-3. Число l, находящееся внутри скобок (то есть -2) обозначает, что мы должны сдвинуть параболу y=ax² на 2 единичных отрезка вправо. Да, именно вправо по числовой прямой Ох. Я это обозначила на чертеже. А вот значение m (то есть - 3) обозначает, что мы должны сдвинуть параболу y=ax² на 3 единичных отрезка вниз по оси Оу. Таким образом, парабола у=ах² приобретает вид у=1(х-2)²-3, просто единицу (а=1) мы не пишем.