Question

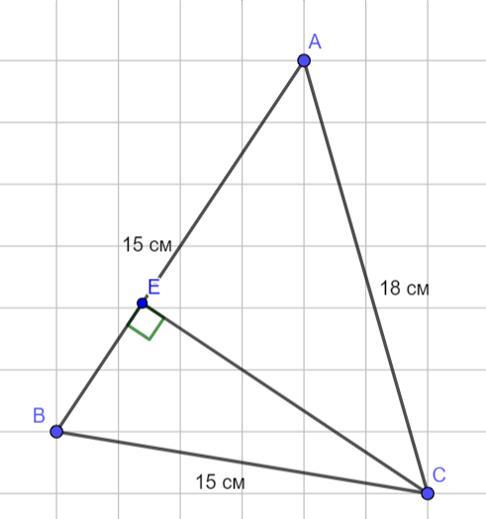
1. Найдите высоту треугольника, проведенную к меньшей стороне, если стороны равны 15 см, 15 см и 18 см.​

Answer 1

Дано:

AB = 15 см;

BC = 15 см;

AC = 18 см;

CE ⊥ AB

Найти:

CE - ?

                                               Решение:

Для решения этой задачи нам понадобятся две формулы, по которым можно найти площадь треугольника:

1) $S = \sqrt{p(p-a)(p-b)(p-c)}$ (формула Герона), где p — это полупериметр,  a,b,c — стороны треугольника.

2) $\displaystyle S = \frac{1}{2} ah_a$, где а — это сторона треугольника, $h_a$ — высота, проведенная к этой стороне.

______________________________________________

Найдем полупериметр данного треугольника и воспользуемся формулой №1, чтобы вычислить площадь:

$\displaystyle p = \frac{AB + BC + AC}{2}= \frac{15 + 15 + 18}{2}=\frac{48}{2}= 24$ (см).

$S _{\triangle ABC} =\sqrt{24(24-15)(24-15)(24-18)}= \sqrt{24\cdot9\cdot 9 \cdot 6} = \\ \\ =\sqrt{2\cdot 2\cdot 2\cdot 3 \cdot 3\cdot 3 \cdot 3 \cdot 3 \cdot 2 \cdot 3}=\sqrt{2^4\cdot 3^6}=\sqrt{2^4}\cdot\sqrt{3^6}=2^2 \cdot 3^3 = 4\cdot 27 = 108$. (см²). ⇒ чтобы удобнее было извлекать корень, мы разложили каждое число в произведении на простые множители, а после одинаковые множители записали в виде степени.

Теперь с помощью формулы №2 составим уравнение, чтобы отыскать CE (высоту треугольника):

$\displaystyle \frac{1}{2} \cdot AB \cdot CE = S_{ABC}$;

$\displaystyle \frac{1}{2} \cdot 15\cdot CE = 108$;

$7,5\cdot CE = 108$;

Найдем неизвестный множитель, разделив произведение на известный множитель:

$CE = 108 : 7,5$;

$CE = 14,4$ (см).

Ответ: 14,4 см.