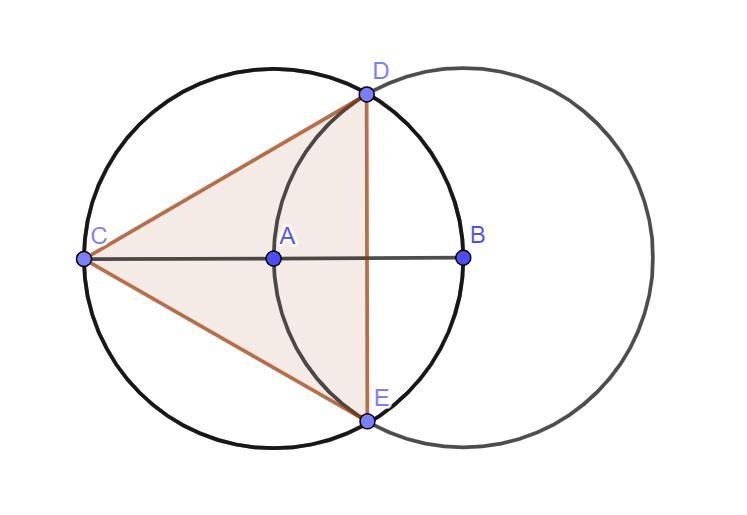
45 баллов, легкая задача. Докажите, что треугольник равносторонний.(см.фото). Радиусы окружностей одинаковы, a и b - центры окружностей
Ответы
Соединим точку В с точками D и Е, и точку А с точками D и Е, получим два равносторонних треугольника АDВ и АВЕ, которые равны по трем сторонам, являющимся одинаковыми радиусами окружностей. АD и АЕ - радиусами окружности с центром в точке А ; ВD и ВЕ - радиусами окружности с центром в точке В, и радиусом АВ, общим для этих окружностей. Значит, все углы в этих двух треугольниках равны по 60°, ∠ЕАD=60°+60°=120°- это центральный угол, опирающийся на дугу ЕD, на нее же опирается и вписанный угол ЕСD, значит, он равен половине этой дуги, т.е. 60°, а треугольник СDЕ равнобедренный, т.к. в нем СD=СЕ - как отрезки касательных, проведенные из одной точки С к окружности с центром В. значит, углы при основании ЕD этого треугольника, равны между собой, т.е. ∠CDЕ =∠СЕD=(180°-60°)/2=60°, отсюда следует, что ΔСDЕ - равносторонний. Доказано.