Предмет: Геометрия,
автор: iclassenenyxno55
Товарищи, прошу помогите.
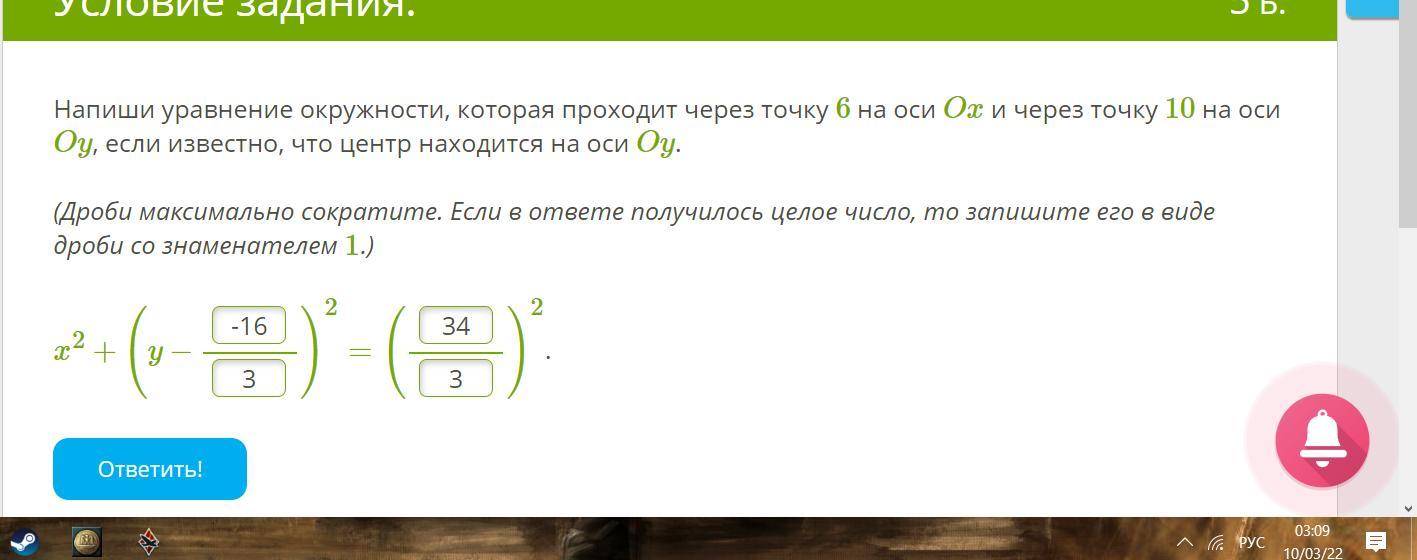
Напиши уравнение окружности, которая проходит через точку 6 на оси Ox и через точку 10 на оси Oy, если известно, что центр находится на оси Oy.
Приложения:
Ответы
Автор ответа:
1
общее уравнение окружности (х-а)²+(у-b)²=R², где (а;b)- центр окружности, R- ее радиус.
подставим данные точки (6;0) и (0;10) в уравнение. получим
если центр на оси оу, то а=0, тогда
(6-0)²+(0-b)²=R²
(0-0)²+(10-b)²=R²
упростим и вычтем из первого уравнения второе.
36+b²-100+20b-b²=0⇒20b=64; b=3.2;
36+b²=R²; R²=10.24+36=46.24=6.8²
искомое уравнение
x²+(у-3.2)²=6.8²
Похожие вопросы
Предмет: Русский язык,
автор: viki109
Предмет: Українська мова,
автор: наталья576
Предмет: Қазақ тiлi,
автор: адильробот
Предмет: Математика,
автор: Аноним
Предмет: Химия,
автор: дережор29