Question

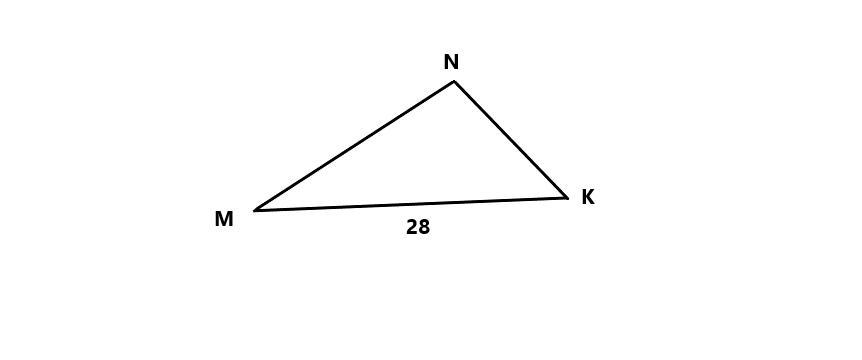
Какова длина стороны MN в треугольнике MNK и площадь MNK , если MK = 28 ∠K=30° ∠N=70° ?


Для расчётов используй калькулятор.


Запиши ответ числами, округлив их до сотых.


NK =

S =

Answer 1

Ответ:

NK = 29,34; MN = 14,9;  SΔ = 205,38 кв. ед.

Пошаговое объяснение:

ДАНО: треугольник MNK

MK = 28

∠K = 30°

∠N = 70°

НАЙТИ:

MN - ?

NK - ?

SΔ - ?

РЕШЕНИЕ:

Сумма углов треугольника 180°. Отсюда,

∠М = 180° - (30° + 70°) = 80°

Искомые стороны найдем с помощью теоремы синусов.

Теорема синусов звучит так: стороны треугольника пропорциональны синусам противолежащих углов.

Запишем выражение для данного треугольника.

$\displaystyle \frac{MK}{sinN} =\frac{NK}{sinM} =\frac{MN}{sinK}$

Из равенства выразим NK и MN:

$\displaystyle NK=\frac{MK*sinM}{sinN}$

$\displaystyle MN=\frac{MK*sinK}{sinN}$

Подставим числовые значения и вычислим с помощью калькулятора. Результат округлим до сотых.

$\displaystyle NK=\frac{28*sin80к}{sin70к}=\frac{28*0,9848}{0,9397} =29,34$

$\displaystyle MN=\frac{28*sin30к}{sin70к}=\frac{28*0,5}{0,9393} =14,9$

Площадь треугольника найдем как половину произведения двух сторон на синус угла между ними.

$\displaystyle Sз=\frac{1}{2} *MK*NK*sinK$

$\displaystyle Sз=\frac{1}{2} *28*NK*sin30к=\frac{1}{2} *28*29,34*0,5=205,38$ (кв. ед.)