Question

СРОЧНО
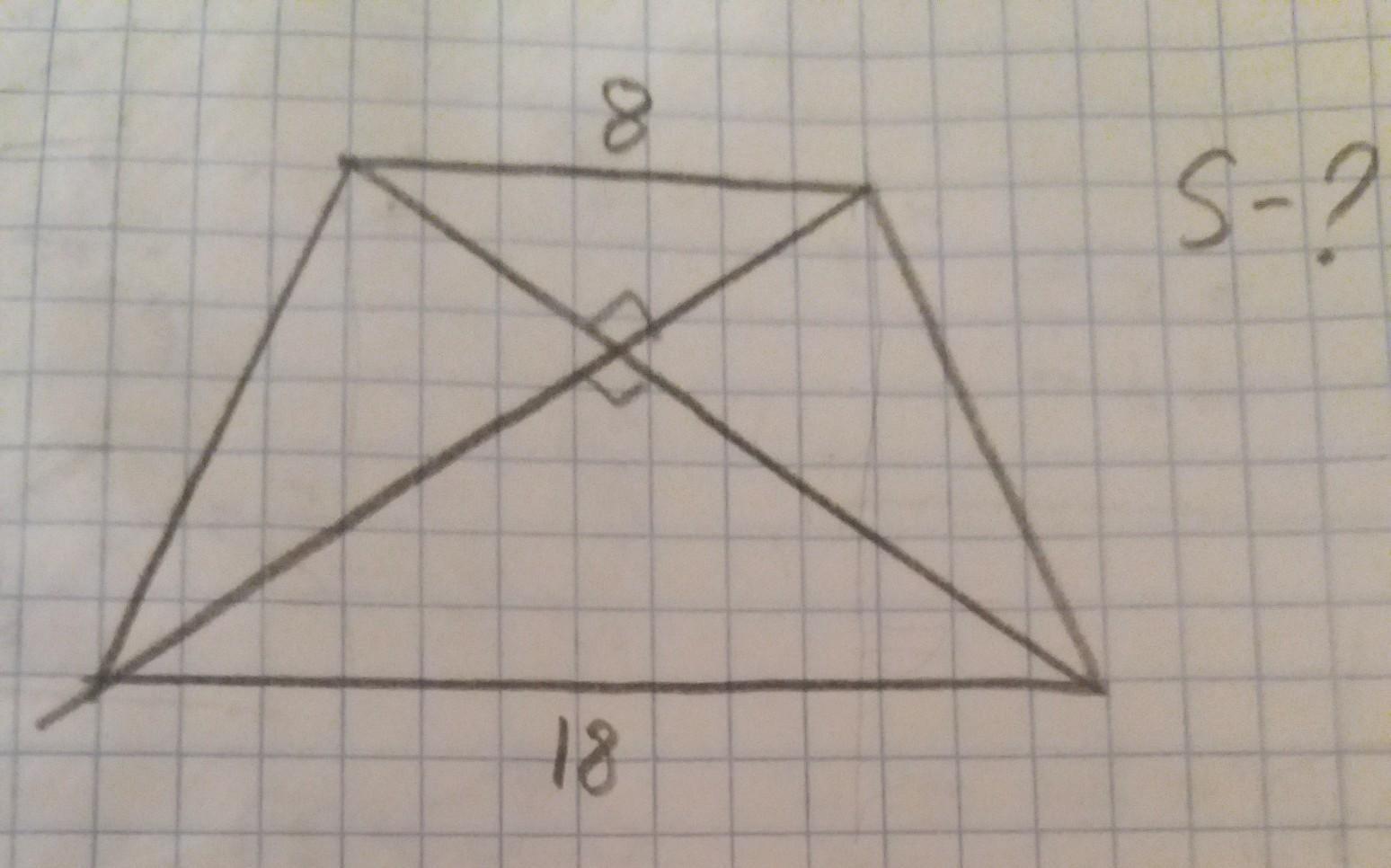
даю 50 баллов, в ответе должно быть 169, нужно ПОЛНОЕ решение, с объяснением на ЛИСТЕ. других данных нет. заранее спасибо!​

Answer 1

Ответ:

S = 169 ед²

Пошаговое объяснение:

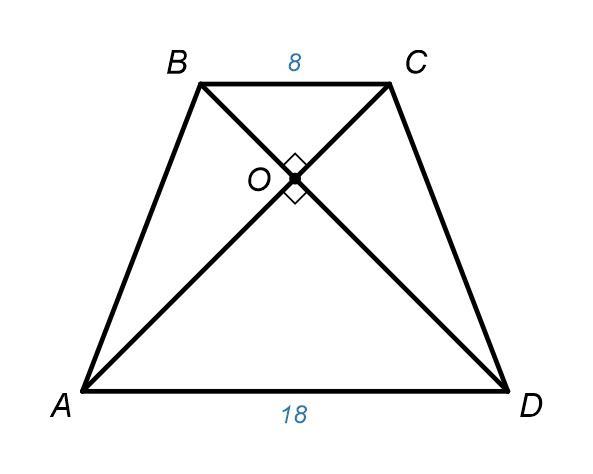
По чертежу видно что это равнобедренная трапеция, у которой AB = CD, ⇒ BO = OC, и AO = OD

Рассмотрим ΔBOC. Это прямоугольный, равнобедренный Δ.

Обозначим BO = OC = x

⇒ по Теореме Пифагора:

$8^{2} = x^{2} + x^{2} \\\\64 = 2x^{2} \\\\x^{2} = \frac{64}{2} \\\\x^{2} = 32\\\\x = \sqrt{32} = \sqrt{16*2} = 4\sqrt{2}$

Рассмотрим ΔAOD. Это прямоугольный, равнобедренный Δ.

Обозначим AO = OD = y

⇒ по Теореме Пифагора:

$18^{2} = y^{2} + y^{2} \\\\324 = 2y^{2} \\\\y^{2} = \frac{324}{2} \\\\y^{2} = 162\\\\y = \sqrt{162} = \sqrt{81*2} = 9\sqrt{2}$

Запишем формулу площади трапеции:

$S = \frac{1}{2}*d_{1}* d_{2}*sin(AOB)$

где d₁ = BD, а d₂ = AC диагонали трапеции.

Т.к. BD = AC ⇒ d₁ = d₂

Найдём длину диагоналей нашей трапеции:

Известно что $BD = AC = x + y = 4\sqrt{2}+9\sqrt{2}=13\sqrt{2}$

∠AOB и ∠BOC - смежные углы, из которых ∠BOC = 90°, а их сумма = 180°

⇒ 180° = ∠AOB + ∠BOC

180° = ∠AOB + 90°

∠AOB = 180° - 90°

∠AOB = 90°

Так же известно что у двух пересекающихся прямых, накрест лежащие углы равны между собой ⇒ ∠BOC = ∠AOD = 90°, и ∠AOB = ∠COD = 90°

т.к. ∠AOB = 90° ⇒ sin(90°) = 1

подставляем полученные значения в формулу площади трапеции:

$S = \frac{1}{2} * 13\sqrt{2} * 13\sqrt{2} * sin(90а) = \frac{(13\sqrt{2} )^{2}}{2} *1 = \frac{13^{2} *(\sqrt{2})^{2}}{2} = \frac{169*2}{2} = 169 eg^{2}$