Предмет: Геометрия,
автор: tatyanaizratova11
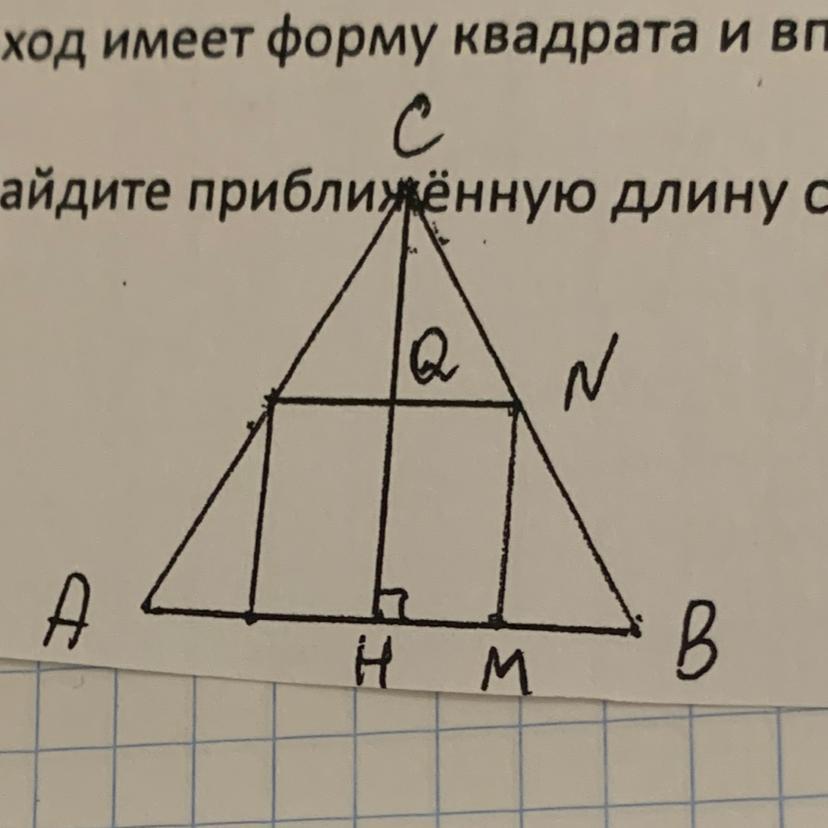
В древнем Египте, как это и положено, строили пирамиду-гробницу для Фараона Среднего царства. Если наклонить одну из сторон пирамиды так, чтобы она стала перпендикулярна полу, то она будет иметь форму равностороннего треугольника со стороной 150 метров. В этой стене строителям требуется проделать отверстие для возможности пройти внутрь и обустроить усыпальницу. Известно, что полученный проход имеет форму квадрата и вписан в треугольник, высота которого делит сторону квадрата пополам. Найдите приближённую длину стороны квадрата, считая, что корень из 3 = 1,73
Приложения:
Ответы
Автор ответа:
6
Ответ:
Объяснение:
Обозначим сторону квадрата NM = x м, тогда QN = x/2 м.
Так как ABC - равносторонний, то угол CNQ = NBM = 60°.
Значит, угол QCN = MNB = 30°, а CQN = NMB = 90°.
Имеем два прямоугольных треугольника:
CNQ с углами 30°, 60° и 90° и с малым катетом QN = x/2 м.
NBM с углами 30°, 60° и 90° и с большим катетом NM = x м.
В треугольнике CNQ гипотенуза
NC = QN/cos 60° = (x/2) : (1/2) = x м.
В треугольнике NBM гипотенуза
BN = MN/sin 60° = x : (√3/2) = 2x/√3 ≈ 1,156x м.
А сумма этих гипотенуз равна стороне треугольника 150 м:
NC + BN = BC
x + 1,156x = 150
2,156x = 150
x = 150/2,156 ≈ 69,571 ≈ 70 м
Похожие вопросы
Предмет: Русский язык,
автор: Anay1505
Предмет: Қазақ тiлi,
автор: макс1916
Предмет: Английский язык,
автор: luizanevskaya
Предмет: Алгебра,
автор: denysmysh
Предмет: Математика,
автор: Zhenya1999