Предмет: Алгебра,
автор: qwertyuiop55
С1
Решить уравнение (1/2)sin2x+sin^2x-sinx=cosx
И указать корни уравнения на отрезке [-2π;-π/2]
Ответы
Автор ответа:
0
Произведение равно нулю, если хотя бы один из множителей равен нулю
(*)
При х=π/2 имеет 1=0 - не верно, значит имеем право разделить левую и правую части уравнения (*) на cosx≠0.
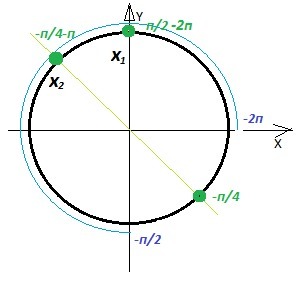
Отбор корней на отрезке [-2π;-π/2].
1. Если n=-1, то
2. Если k=-1, то
Автор ответа:
0
Kорни уравнения на отрезке [-2π;-π/2]. Выбор корней на единичной окружности.
x₁ = -3π/2; x₂ = -5π/4;
Приложения:
Похожие вопросы
Предмет: Химия,
автор: wonderphoenix
Предмет: Қазақ тiлi,
автор: arlansatybaldy
Предмет: Информатика,
автор: charliexhazbin
Предмет: Математика,
автор: rrrrtttttt
Предмет: Математика,
автор: krukov02