Question

Из одной точки к плоскости β проведены перпендикуляр и наклонная. Длина наклонной 17 см, длина перпендикуляра 15 см. Найдите длину проекции этой наклонной на плоскость β.

Из одной точки к плоскости β проведены перпендикуляр и наклонная. Длина наклонной 2,06 м. Угол между наклонной и ее проекцией на плоскость β равен 60 градусам. Найдите длину перпендикуляра.

Из одной точки к плоскости β проведены перпендикуляр и наклонная. Длина наклонной 50 м, длина проекции этой наклонной на плоскость β 30м. Найдите длину перпендикуляра.

Из одной точки к плоскости β проведены перпендикуляр и наклонная. Длина перпендикуляра 0,8 дм. Длина проекции наклонной на плоскость β - 0,6 дм. Найдите длину наклонной.

Из одной точки к плоскости β проведены перпендикуляр и наклонная. Угол между ними равен 60 градусам. Длина наклонной 1,25м. Найдите длину перпендикуляра.

Answer 1

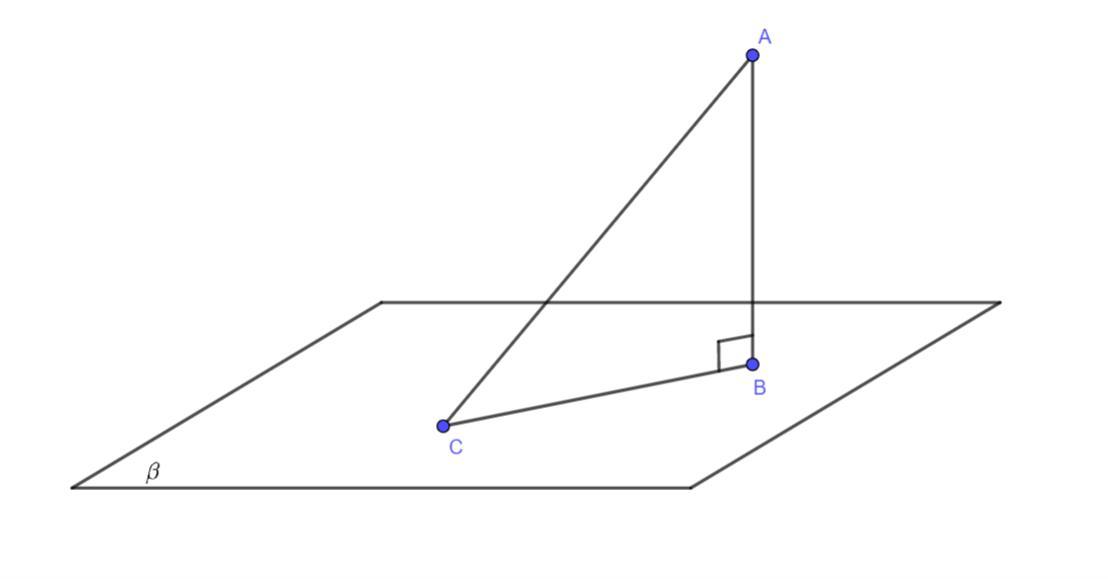
AB ⊥ β — перпендикуляр;

AC — наклонная к плоскости β.

BC — проекция наклонной AC на плоскость β.

Δ ABC — прямоугольный (∠B = 90°).

_____________________

• Задание №1

Дано: AC = 17 см; AB = 15 см.

Найти: BC.

Решение:

Рассмотрим прямоугольный треугольник ABC.

По теореме Пифагора:

AC² = AB² + BC²

BC² = AC² - AB²

BC² = 17² - 15² = 64

Отсюда, BC = √64 = 8 (см).

Ответ: 8 см.

• Задание №2

Дано: AC = 2,06 м; ∠C = 60°.

Найти: AB.

Решение:

Рассмотрим прямоугольный треугольник ABC.

Синус острого угла равен отношению противолежащего катета к гипотенузе, поэтому:

$\displaystyle sin \angle C = \frac{AB}{AC}$

$\displaystyle sin 60\textdegree = \frac{AB}{2,06}$

$\displaystyle \frac{\sqrt{3} }{2} = \frac{AB}{2,06}$

$\displaystyle AB = \frac{2,06\cdot \sqrt{3} }{2} = 1,03\cdot \sqrt{3} \approx 1,03\cdot 1,73 \approx 1,78$ (м).  

Ответ: 1,78 м.

• Задание №3

Дано: AC = 50 м; BC = 30 м.

Найти: AB.

Решение:

Рассмотрим прямоугольный треугольник ABC.

По теореме Пифагора:

AC² = AB² + BC²

AB² = AC² - BC²

AB² = 50² - 30² = 1600

Отсюда, AB = √1600 = 40 (м).

Ответ: 40 м.

• Задание №4

Дано: AB = 0,8 дм; BC = 0,6 дм.

Найти: AC.

Решение:

Рассмотрим прямоугольный треугольник ABC.

По теореме Пифагора:

AC² = AB² + BC²

AC² = 0,8² + 0,6² = 1

Отсюда, AC = √1 = 1 (дм).

Ответ: 1 дм.

• Задание №5

Дано: AC = 1,25 м; ∠A = 60°.

Найти: AB.

Решение:

Рассмотрим прямоугольный треугольник ABC.

Косинус острого угла равен отношению прилежащего катета к гипотенузе, поэтому:

$\displaystyle cos\angle A = \frac{AB}{AC}$  

$\displaystyle cos 60 \textdegree = \frac{AB}{1,25}$

$\displaystyle \frac{1}{2} = \frac{AB}{1,25}$

AB = 1,25 : 2 = 0,625 (м).

Ответ: 0,625 м.