Question

Радиус вписанной окружности прямоугольного треугольника равен 5, а один из катетов – 15. Найти площадь треугольника

Answer 1

${}$

Упростим себе задачу, заменив треугольник на подобный ему, но с линейными элементами, в 5 раз меньшими. У такого треугольника радиус вписанной окружности равен 1, а один из катетов равен 3.

Как известно, радиус вписанной окружности в прямоугольный треугольник равен $r=p-c=\dfrac{a+b-c}{2},$ откуда (считая, что катет a=3, b - второй катет, а c - гипотенуза)

$3+b-c=2; c=b+1.$

Остается воспользоваться теоремой Пифагора:

$c^2=a^2+b^2;\ (b+1)^2=9+b^2;\ b^2+2b+1=9+b^2;\ b=4;\ c=5;$

$S=pr=\dfrac{a+b+c}{2}\cdot r=\dfrac{3+4+5}{2}\cdot 1=6.$

Остается вернуться к исходному треугольнику, помня, что площади подобных фигур относятся как квадрат коэффициента подобия. Поэтому 6 надо умножить на 5 в квадрате.

Ответ: 150

Answer 2

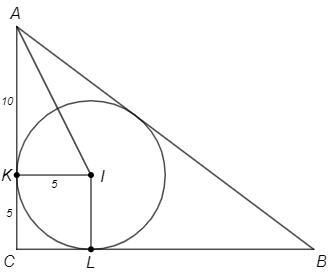
Центр вписанной окружности (I) - точка пересечения биссектрис. ∠KAI=∠A/2

K, L - точки касания. Радиус в точку касания перпендикулярен касательной. ∠L=∠K=90°

CKIL - квадрат. CK=IK=5; AK=10

tg(A/2) =tg(KAI) =IK/AK =5/10 =1/2

$tgA=\frac{2tg\frac{A}{2}}{1-tg^{2}\frac{A}{2}}=\frac{2*\frac{1}{2}}{1-\frac{1}{4}}=\frac{4}{3}$

BC =AC tgA =15 *4/3 =20

S =1/2 AC*BC =1/2 *15 *20 =150