Question

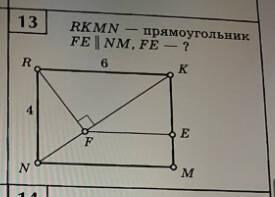
RKMN - прямоугольник

FE || NM, найти FE

Answer 1

Ответ:

• $\displaystyle \boldsymbol{FE=4\frac{2}{13} }$ ед.

Объяснение:

RKMN - прямоугольник, тогда RK=NM=6, NR=NK=4, ∠NRK=∠RKM=∠KMN=∠MNR=90°.

• Теорема Пифагора: Квадрат гипотенузы равен сумме квадратов катетов.

ΔNRK - прямоугольный, т.к. ∠NRK=90°.

Тогда по т. Пифагора:

$\boldsymbol{NK}=\sqrt{NR^2+RK^2} =\sqrt{4^2+6^2}=\sqrt{16+36}=\boldsymbol{2\sqrt{13}}$ед.

• Квадрат катета равен произведению его проекции на гипотенузу.

$RK^2=FK\cdot NK$, откуда $\displaystyle \boldsymbol{FK}=\frac{RK^2}{NK} =\frac{6^2}{2\sqrt{13} } =\frac{36}{2\sqrt{13} } =\boldsymbol{\frac{18}{\sqrt{13} } }$ ед.

• В треугольнике прямая, параллельная основанию, отсекает треугольник, подобный данному.

Т.к. $FE||NM$ по условию, то $\triangle NKM \sim \triangle FKE$, тогда $\displaystyle \frac{NK}{FK}=\frac{NM}{FE}$, откуда $\displaystyle \boldsymbol{FE}=\frac{FK\cdot NM}{NK} =\frac{\frac{18}{\sqrt{13} }\cdot 6 }{2\sqrt{13} } =\frac{18\cdot 6}{2\sqrt{13}\cdot \sqrt{13} } =\frac{9\cdot 6}{13} =\frac{54}{13} =\boldsymbol{4\frac{2}{13} }$ ед.