АЛГЕБРА 10 КЛАСС ТЕМА ПРОИЗВОДНЫЕ ПОМОГИТЕ СРОЧНО РЕШИТЬ ПОЖАЛУЙСТА
Ответы
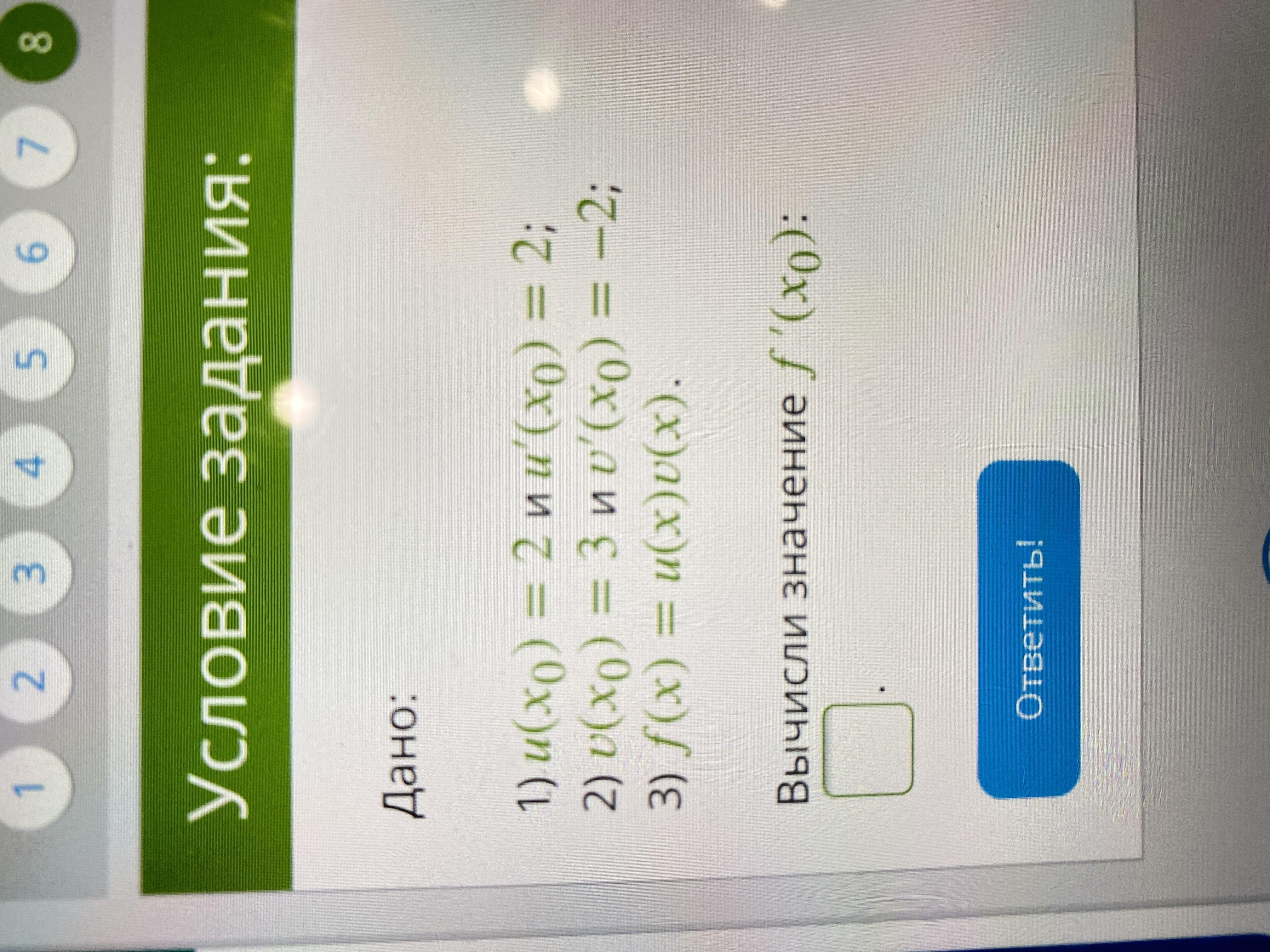
Ответ:
уроке мы вспомним, что такое производная функции, разберемся, как вычислять производные некоторых функций, вспомним геометрический и физический смысл производной.
Если у вас возникнет сложность в понимании темы, рекомендуем посмотреть урок «Производная и интеграл»
Определение производной функции
Производная функции в точке :
Геометрический смысл производной
Если задан график функции , то производная в точке – это тангенс угла наклона касательной к данной функции в точке c абсциссой (или угловой коэффициент касательной).
Физический смысл производной
Если в качестве функции мы берем перемещение, зависящее от , – , то , где – перемещение, – время, а – мгновенная скорость в данной точке.
И сегодня мы попробуем вычислить некоторые производные по определению.
Производная функции
Начнем с самого простого – с линейной функции.
Пусть , где и – некоторые числа, а – переменная.
Тогда:
Итак, выясняется, что для любого . Значит, можно утверждать, что .
О чем это говорит?
Во-первых, мы подтвердили несколько фактов про линейную функцию, которые нам, возможно, уже были известны.
1. Так, исходя из геометрического смысла производной, тангенс угла наклона прямой совпадает с ее угловым коэффициентом (он равен производной в соответствующей точке).
Кроме этого, мы видим, что раз производная постоянна,