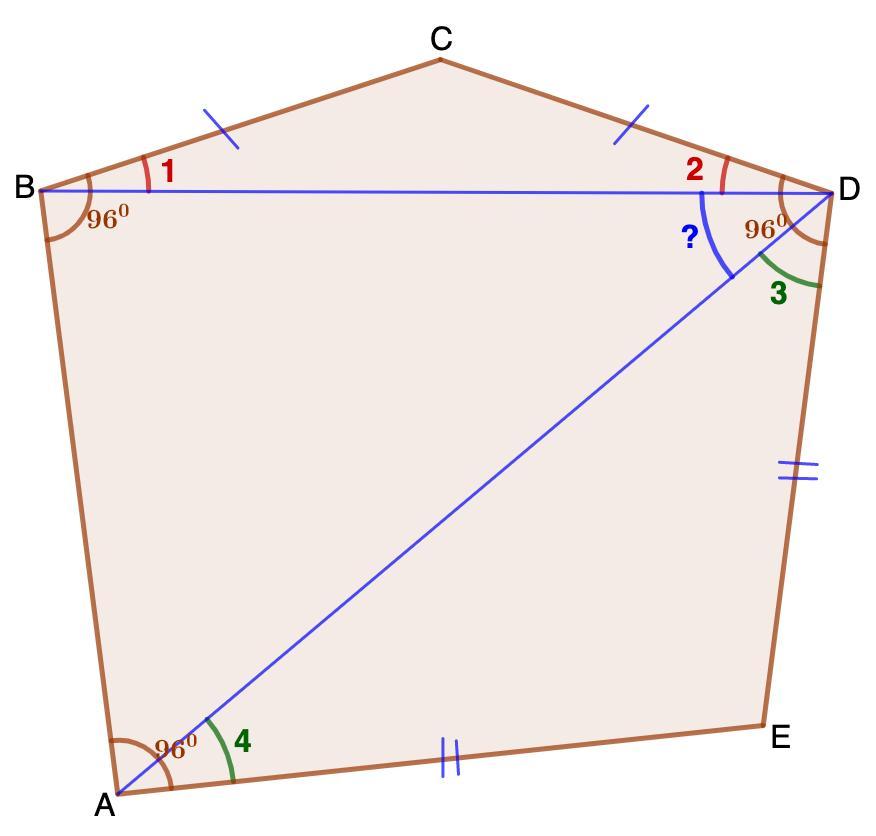
В пятиугольнике ABCDE углы EAB, ABC и CDE равны 96 градусов. Найти градусную меру угла ADB, если BC=CD, a DE=AE
Ответы
Ответ:
Градусная мера угла ADB равна 42°.
Пошаговое объяснение:
Требуется найти градусную меру угла ADB.
Дано: ABCDE - пятиугольник;
∠EAB = ∠ABC = ∠CDE = 96°;
BC=CD, DE=AE.
Найти: ∠ADB.
Решение:
1. Найдем сумму углов С и Е.
- Сумма углов многоугольника равна (n-2)·180°.
Сумма углов данного пятиугольника ABCDE равна:
(5 - 2) · 180° = 540°
Три угла нам известны:
∠EAB + ∠ABC + ∠CDE = 96° · 3 = 288°
⇒ ∠С + ∠Е = 540° - 288° = 252°
2. Рассмотрим ΔBCD и ΔADE;
BC=CD, DE=AE (по условию)
⇒ ΔBCD и ΔADE - равнобедренные.
- Углы при основании равнобедренного треугольника равны.
⇒ ∠1 = ∠2; ∠3 = ∠4.
- Сумма углов треугольника равны 180°.
Найдем сумму углов двух треугольников ΔBCD и ΔADE:
∠1 + ∠С + ∠2 + ∠3 +∠Е + ∠4 = 180° + 180°
или
(∠1 + ∠4) + (∠2 + ∠3) +(∠С + ∠Е) = 360°
Так как ∠1 = ∠2; ∠3 = ∠4, то
(∠1 + ∠4) = (∠2 + ∠3)
∠С + ∠Е = 252°
Получим выражение:
2 · (∠2 + ∠3) + 252° = 360
2 · (∠2 + ∠3) = 360° - 252° |:2
∠2 + ∠3 = 54°
3. ∠СDE = 96°
∠ADB = ∠СDE - (∠2 +∠3) = 96° - 54° = 42°
Градусная мера угла ADB равна 42°.