Question

Периметр основания правильной треугольной призмы равен 12 V3 см. Диагональ боковой грани составляет с плоскостью основания угол 30°. Найдите объем призмы.

Answer 1

Формула объема призмы:

V = S ∙ h, где S — площадь основания, h — высота (которая у прямой призмы совпадает с боковым ребром).

Тогда в нашем случае:  

$V_{ABCA_1B_1C_1} = S_{\triangle ABC} \cdot B_1B$.

• Вычислим $S_{\triangle ABC}$:

Основанием правильной треугольной призмы является правильный треугольник (то есть у него все стороны равны).

В таком случае, если $P_{ABC} = 12\sqrt{3}$ см, то:

$AB = 12\sqrt{3} : 3 = 4\sqrt{3}$ (см).

Формула площади равностороннего треугольника:

$\displaystyle S=\frac{a^2\sqrt{3} }{4}$, где а — его сторона.

Отсюда, $S_{\triangle ABC} = \frac{(4\sqrt{3})^2\cdot\sqrt{3} }{4} = \frac{16\cdot 3 \cdot \sqrt{3} }{4} = 12\sqrt{3}$ (см²).

• Вычислим длину $B_1B$:

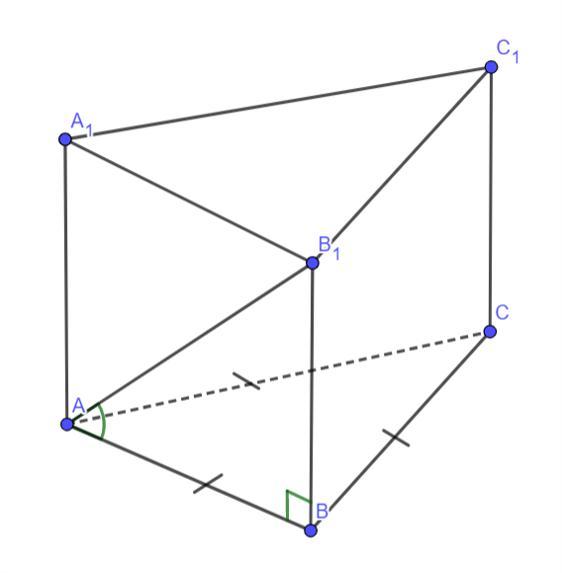
∠B₁AB = 30°— угол между диагональю боковой грани B₁A и (ABC).

Рассмотрим прямоугольный ΔB₁AB (∠B₁BА = 90°).

Тангенс острого угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему:

$\displaystyle tg \angle B_1AB = \frac{B_1B}{AB} .$

Выразим отсюда B₁B:

$\displaystyle B_1B = AB \cdot tg \angle B_1AB = 4\sqrt{3} \cdot tg 30 \textdegree = 4\sqrt{3} \cdot \frac{\sqrt{3} }{3} = \frac{4\sqrt{3} \cdot \sqrt{3} }{3}= \frac{4\cdot 3}{3}= 4$ (см).

Подставим полученные значения в формулу и вычислим объем:

$V_{ABCA_1B_1C_1} = 12\sqrt{3} \cdot 4= 48\sqrt{3}$ (см³).

Ответ: $48\sqrt{3$ см³.