Question

СРОЧНО НУЖНА ПОМОЩЬ!!!
ДАЮ 50 БАЛЛОВ

Answer 1

Ответ:

(x + 15/2)² + y² = (25/2)²

Объяснение:

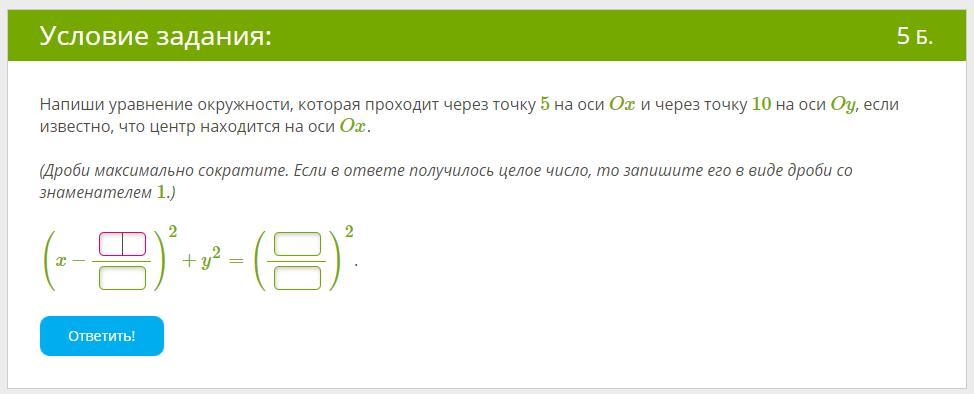
Напиши уравнение окружности, которая проходит через точку 5 на оси Ox и через точку 10 на оси Oy, если известно, что центр находится на оси Ox.


Пусть абсцисса центра окружности а.

Тогда, так как центр окружности лежит на оси оХ, координаты центра (а;0)

Если обозначить радиус окружности как r, то уравнение окружности:

(x - a)² + (y - 0)² = r²

или (х - а)² + y² = r²

Окружность проходит через точки с координатами (5;0) и (0;10)

Значит эти  координаты должны удовлетворять уравнению окружности.

Тогда получается система уравнений:

(5 - а)² + 0² = r²

(0 - a)² + 10² = r²

Решив совместно уравнения этой системы можно определить а и r.

Вычитая из верхнего уравнения нижнее и раскрывая скобки:

25 - 10a + a² - a² - 100 = 0

a = -75/10

Из верхнего уравнения следует:

r = |5 - a| = |5 + 75/10| = 125/10

Теперь можно записать уравнение окружности:

(x + 75/10)² + y² = (125/10)²

Можно, конечно, записать в десятичных дробях:

(x + 7.5)² + y² = 12.5²

Или хотя бы сократить дроби 75/10 = 15/2 и 125/10 = 25/2

Тогда (x + 15/2)² + y² = (25/2)² - это ответ т.к просят сократить