Предмет: Алгебра,
автор: trofimcom2000
Найти интеграл. Помогите пожалуйста.В 3) 1 раз sin и cos там ошибка
Приложения:
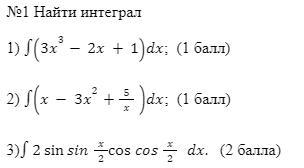
Ответы
Автор ответа:
0
Ответ:
Вычислили интегралы:
1)
2)
3)
Объяснение:
Требуется вычислить интегралы.
- Интеграл суммы равен сумме интегралов.
Используем формулу:
Добавим еще одну формулу:
Данный интеграл можно вычислить методом замены переменной.
Получим:
Выполним обратную замену:
trofimcom2000:
в 1 не 2x^3, а 3x^3
и 3 тоже не правильно
Похожие вопросы
Предмет: Русский язык,
автор: fisenckodaria2
Предмет: Русский язык,
автор: 111585
Предмет: Русский язык,
автор: yusuprun
Предмет: Химия,
автор: fedy742323