Предмет: Алгебра,
автор: ellis0440
найти сумму всех целых решений неравенств, с решением пожалуйста
Приложения:
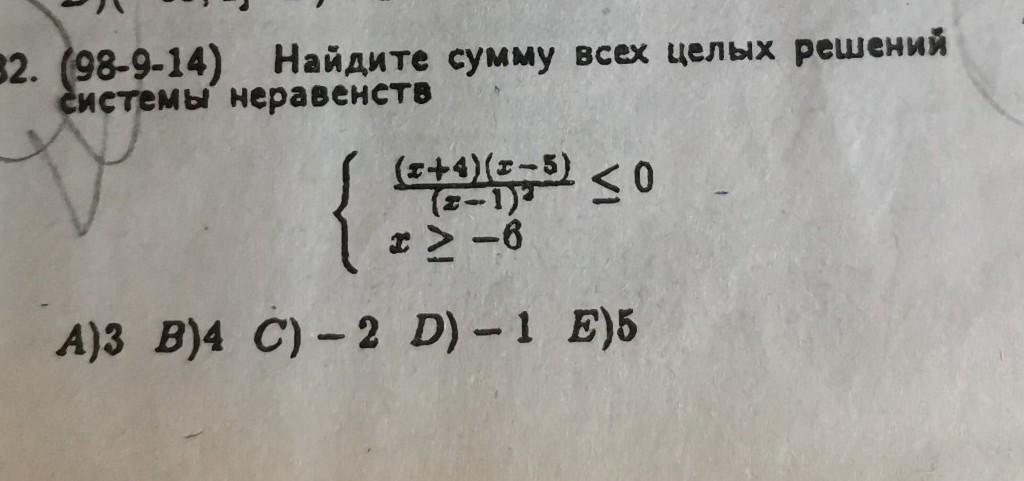
Ответы
Автор ответа:
0
Ответ:
A)3
Объяснение:
//Так как в знаменателе получится 0, и не будет решений
Разберемся с одним неравенством:
Домножим обе части уравнения на (x-1)²:
Решаем квадратное уравнение как удобно:
В первой системе пустое множество(нет пересечений)
Во второй системе: [-4,5].
Соединим всё:
Находим ПЕРЕСЕЧЕНИЕ(∩):
Так как , то:
[-4,1) ∪ (1,5]
И их сумма равна = -4+1+1+5 = 3
Похожие вопросы
Предмет: Окружающий мир,
автор: Iana1111
Предмет: Русский язык,
автор: kita89116697863
Предмет: Русский язык,
автор: Марк1123
Предмет: Химия,
автор: ypuu
Предмет: Математика,
автор: pypsi73