Предмет: Геометрия,
автор: Kirilovitch
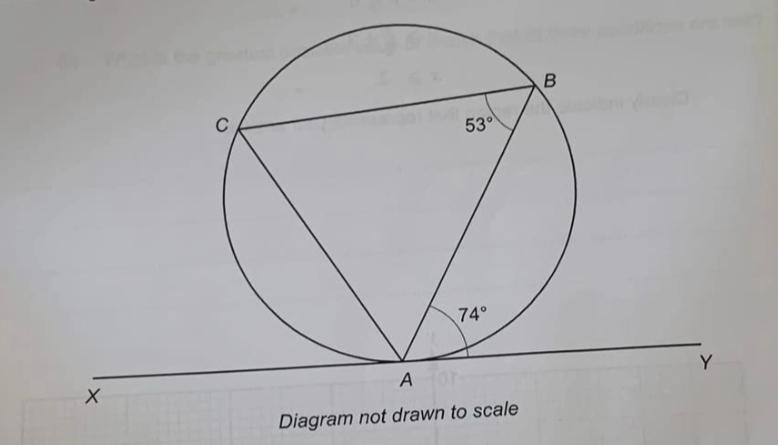
B и C - это точки на окружности круга. XY - касательная к окружности в точке A. BAY = 74 и ABC = 53 Доказывают, что треугольник ABC является равнобедренным треугольником. Вы должны указать причину любого заявления, которое вы делаете, или любого выполняемого вами расчета.
Приложения:
Ответы
Автор ответа:
1
В и С — точки на окружности. Прямая XY касается окружности в точке A. BAY = 74° и ABC = 53°. Докажите, что треугольник ABC равнобедренный. Решение обоснуйте.
Объяснение
Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами. =>
Дуга ВА=74°•2=148°
Величина вписанного угла равна половине величины дуги, на которую опирается. =>
Дуга АС= ∠ АВС•2=53•2=106°
Градусная мера круга равна 360º =>
Дуга ВС=360°-(106°+148°)=106°=>
Угол САВ опирается на дугу ВС и равен половине её градусной меры. ∠САВ=106°:2=53°
∠САВ=∠СВА
Если в треугольнике два угла равны, то этот треугольник — равнобедренный.
∆ АВС равнобедренный, АС=АВ.
Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Русский язык,
автор: gaschimovaesmi
Предмет: Русский язык,
автор: Cady
Предмет: Алгебра,
автор: growdan24
Предмет: Алгебра,
автор: ladynatalia15042005