Предмет: Математика,
автор: yurixxx4662
В правильной треугольной пирамиде PABC отрезок СН – медиана треугольника АВС, точка Y € CH. Докажите, что прямая PY перпендикулярна прямой AB.
Ответы
Автор ответа:
1
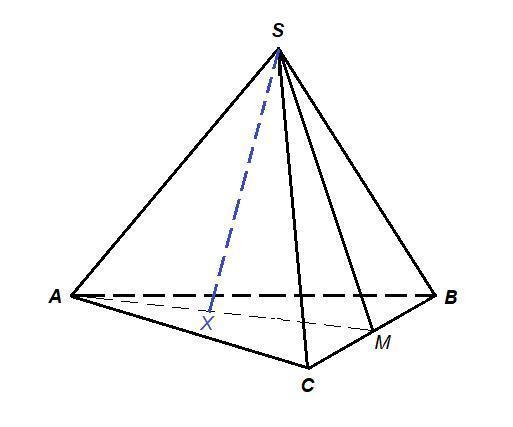
SABC - правильная треугольная пирамида, значит ее основание - правильный треугольник, а боковые грани - равные равнобедренные треугольники.
АМ - биссектриса ΔАВС, значит она и медиана и высота,
AM⊥ВС.
SM⊥BC, как медиана и высота равнобедренного треугольника SBC.
Признак перпендикулярности прямой и плоскости:
если прямая перпендикулярна двум пересекающимся прямым плоскости, то она перпендикулярна плоскости.
ВС⊥АМ, ВС⊥SM, значит ВС⊥(SAM).
Тогда ребро ВС перпендикулярно любой прямой, лежащей в этой плоскости.
SX⊂(SAM), ⇒ BC⊥SX.
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: мус74
Предмет: Английский язык,
автор: kuzhnaeva83
Предмет: Қазақ тiлi,
автор: xusanovjas
Предмет: Химия,
автор: PetrKalash
Предмет: Английский язык,
автор: ankostayeva