Даю 100 баллов!!! Две задачи по геометрии ОГЭ
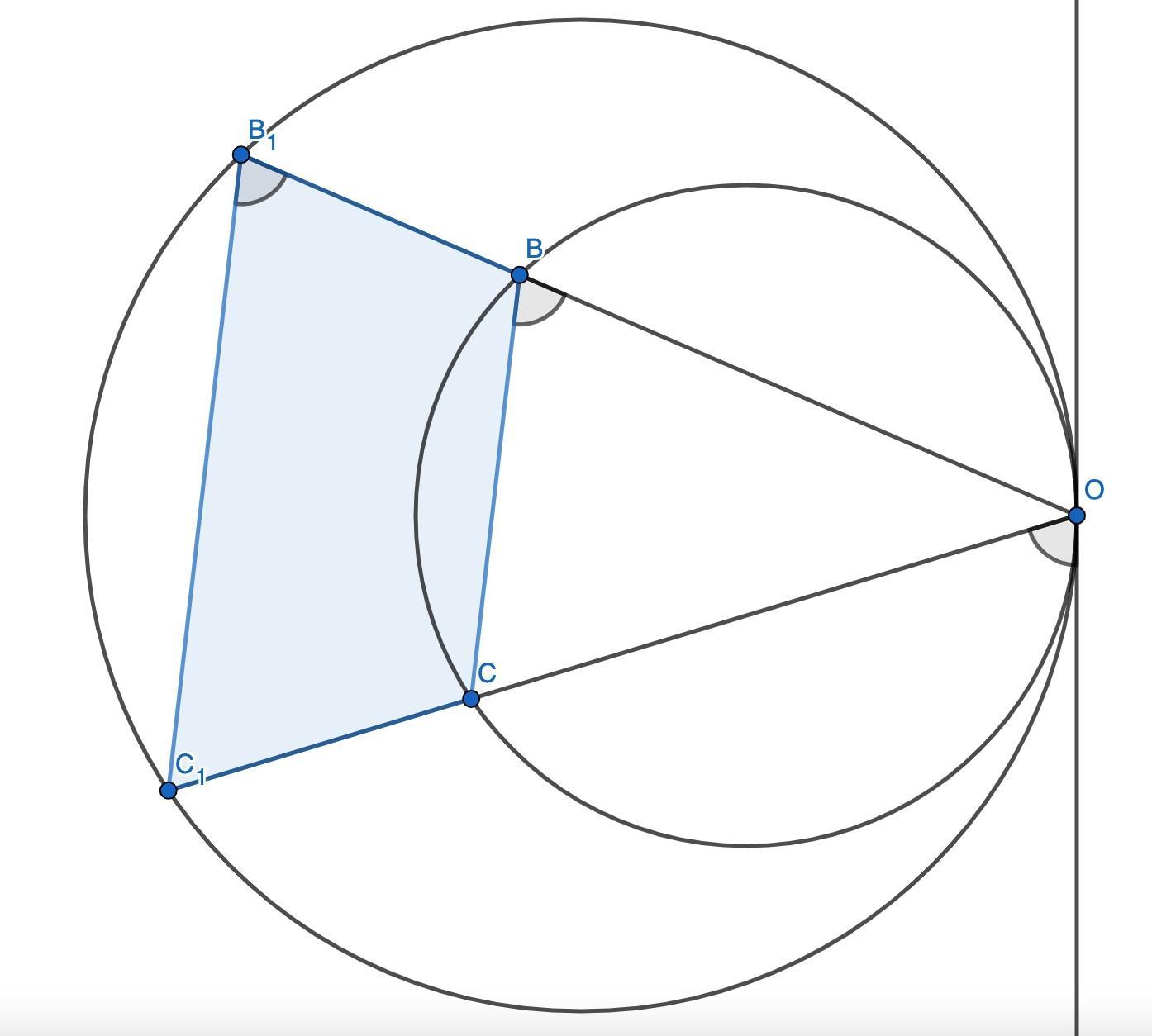
24.Окружности, радиусы которых равны r и R, касаются внутренним образом в точке O. Продолжение хорды OB меньшей окружности пересекают большую окружность в точке B1, а продолжение хорды OC меньшей окружности пересекает большую окружность в точке C1. Докажите, что четырехугольник BB1C1C - трапеция.
25.В трапеции ABCD, BC || AD, биссектрисы угла D перпендикулярна боковой стороне AB и пересекает ее в точке F. Найдите отношение площади четырехугольника BCDF к площади треугольника AFD, если AF:FB = 2:1
Ответы
Ответ:
25. 7 : 8
Объяснение:
24. Проведём общую касательную к окружностям в точке O. Для меньшей окружности угол между касательной и хордой OC равен половине дуги OC, то есть равен вписанному углу ∠OBC. Для большей окружности угол между касательной и хордой OC₁ равен половине дуги OC₁, то есть равен вписанному углу ∠OB₁C₁. Поскольку хорды OC и OC₁ лежат на одной прямой, угол между касательной и этими хордами один и тот же. Углы ∠OBC и ∠OB₁C₁ равны одному и тому же углу, значит, они равны между собой. Тогда BC || B₁C₁.
По теореме синусов . Поскольку радиусы не равны, то и BC ≠ B₁C₁.
Противолежащие стороны четырёхугольника параллельны и не равны, следовательно, это трапеция, что и требовалось доказать.
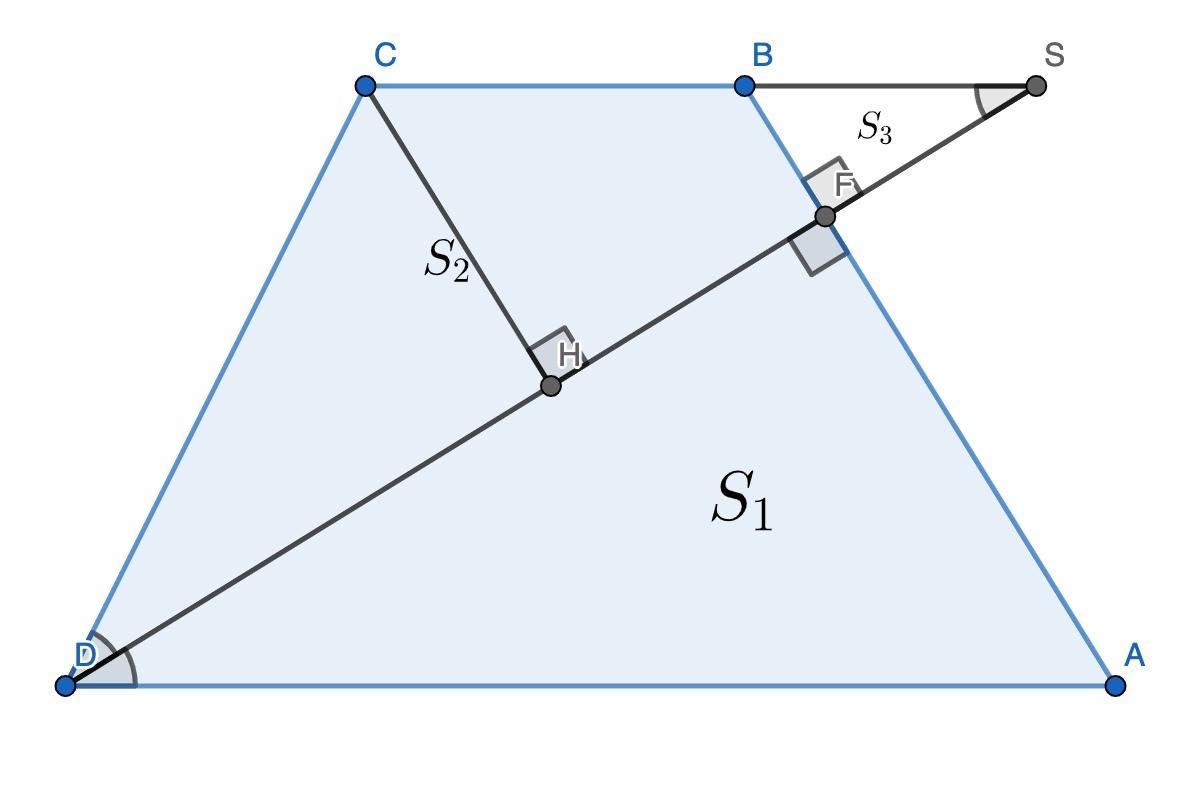
25. Продлим биссектрису DF до пересечения с прямой BC (точку пересечения обозначим S), проведём высоту CH в треугольнике DCS. Обозначим площади следующим образом: .
Заметим, что ∠ADS = ∠DSC как накрест лежащие, ∠ADS = ∠SDC по условию. Тогда ∠DSC = ∠SDC ⇒ треугольник DCS равнобедренный ⇒ DH = HS.
Треугольники ADF и BSF подобны по вертикальным углам ∠AFD и ∠BFS и накрест лежащим углам ∠ADF и ∠FSB с коэффициентом подобия k = AF : FB = 2. Тогда и DF : FS = 2, а .
Треугольники CHS и BFS подобны по общему углу ∠S и соответственным прямым углам ∠CHS и ∠BFS. Коэффициент подобия . Тогда
.
CH — медиана треугольника DCS, значит, . Но
.
Искомое отношение .