Предмет: Алгебра,
автор: home1245
Найти производную функции y = 5x^2 - 2/√x + sin π/4
Приложения:
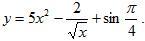
Ответы
Автор ответа:
1
Ответ:
anik200579:
здравствуйте можете помочь с алгеброй вопрос в профиле
МНЕ ПОМОГИТЕ ПОЖАЛУЙСТА ВОПРОС В ПРОФИЛЯ
Похожие вопросы
Предмет: Қазақ тiлi,
автор: asolmax
Предмет: Русский язык,
автор: эвелина610
Предмет: Русский язык,
автор: егор89ковалев
Предмет: Математика,
автор: xusnutdinov2006
Предмет: Литература,
автор: Nikosik384