Question

Помогите чем можете, срочно нужна оценка для 4ки в четверти!!!!

Answer 1

Задание 1.

ответ:

$a_1 = \bf - 3\\ a_2 = \bf 1\\ a_3 = \bf5 \\ a_4 = \bf 9\\ a_{10} = \bf33$

объяснение:

вычислим первые четыре члена и 10-й член арифметической прогрессии, общая формула которой

$a_n = 4n - 7$

для этого подставим значения 1,2,3,4 и 10 по порядку в эту формулу:

$a_1 = 4 \times 1 - 7 = 4 - 7 = - 3$

$a_2 = 4 \times 2 - 7 = 8 - 7 = 1$

$a_3 = 4 \times 3 - 7 = 12 - 7 = 5$

$a_4 = 4 \times 4 - 7 = 16 - 7 = 9$

$a_{10} = 4 \times 10 - 7 = 40 - 7 = 33$

Задание 2.

ответ:

$s _{10} = \bf410$

объяснение:

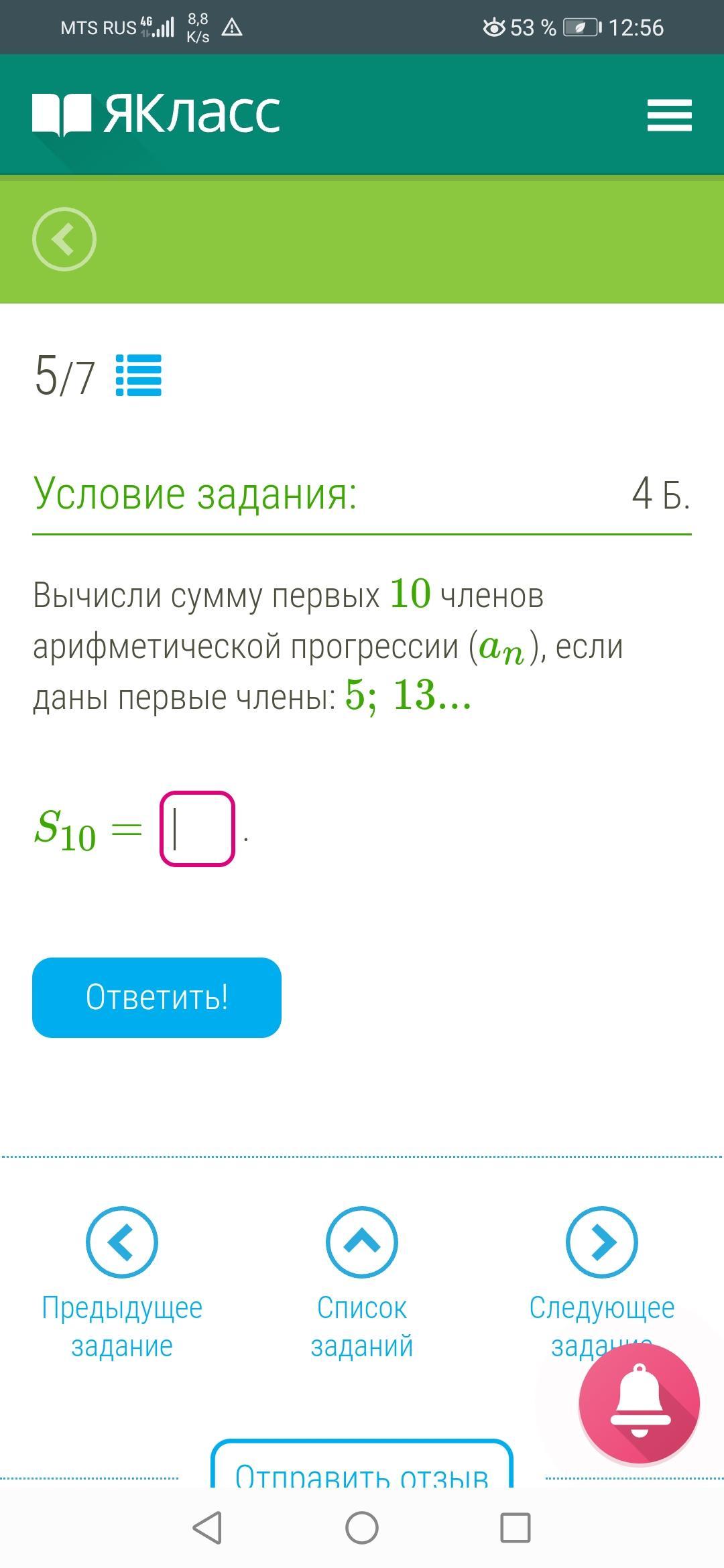
вычислим сумму первых 10 членов арифметической прогрессии, если даны первые члены: 5; 13...

• для начала вычислим d, разность арифметической прогрессии: 13-5=8
• теперь вычислим 10-й член этой прогрессии по формуле n-го члена
• $a_n = a_1 + (n - 1)d$

$a_{10} = 5 + (10 - 1) \times 8 = 5 + 8 \times 9 = 5 + 72 = 77$

• вычислим сумму первых 10 членов по формуле суммы n-го члена арифметической прогрессии:
• $s _{n} = \frac{n(a _1 + a _n) }{2}$

$s_{10} = \frac{10(5 + 77)}{2} = \frac{10 \times 82}{2} = \frac{820}{2} = 410$

Задание 3.

ответ:

$a_3 = \bf16.6 \\ a_4 = \bf 20.4 \\ s _4 = \bf 58.8$

объяснение:

вычислим следующие два члена арифметической прогрессии и сумму первых четырех членов, если ее первый член равен 9, а второй равен 12,8

• вычислим разность арифметической прогрессии: 12,8-9=3.8
• вычислим по формуле n-го члена, приведенной выше, третий и четвертый члены этой прогрессии:

$a_ 3 = 9 + (3 - 1) \times 3.8 = 9 + 2 \times 3.8 = 9 + 7.6 = 16.6$

$a_4 = 9 + (4 - 1) \times 3.8 = 9 + 3 \times 3.8 = 9 + 11.4 = 20.4$

• теперь вычислим сумму первых четырех членов этой прогрессии, по формуле n-го члена, также приведенной выше:

$s_4 = \frac{4(9 +20.4) }{2} = 2 \times 29.4 = 58.8$

Задание 4.

ответ:

$a_{10} = \bf58$

объяснение:

вычислим 10-й член арифметической прогрессии, если известно, что ее первый член равен -1,4, а разность равна 6.6.

для этого подставим известные значения в формулу n-го члена арифметической прогрессии:

$a_{10} = - 1.4 + (10 - 1) \times 6.6 = - 1.4 + 9 \times 6.6 = - 1.4 + 59.4 = 58$

Задание 7.

ответ:

$a_4 = \bf 10$

объяснение:

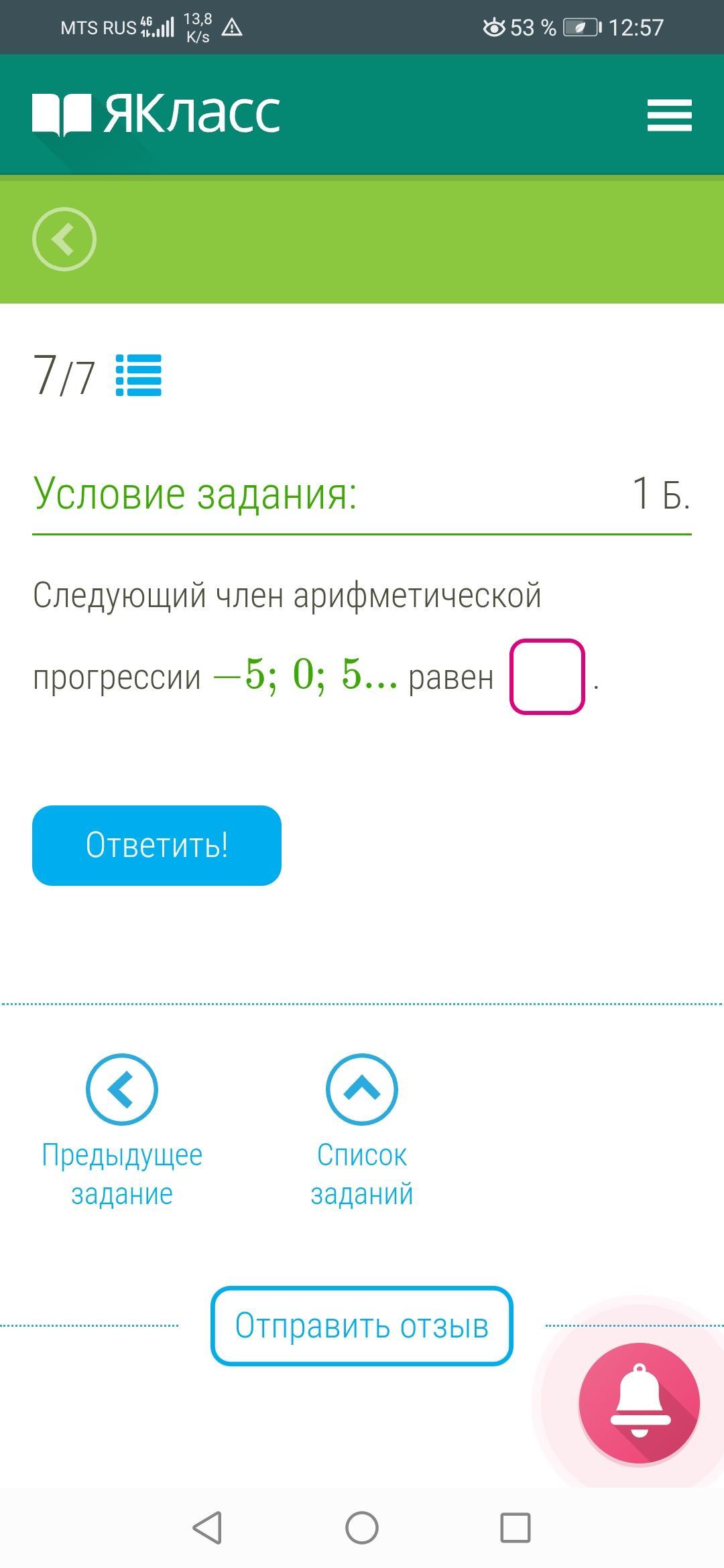
вычислим следующий член арифметической прогрессии -5; 0; 5, для этого:

• найдем ее разность: d=0-(-5)=0+5=0;
• вычислим четвертый член данной арифметической прогрессии, подставив известные значения в формулу n-го члена:
• $a_4 = - 5 + (4 - 1) \times 5 = - 5 + 3 \times 5 = - 5 + 15 = 10$