решите под а
помогите срочно
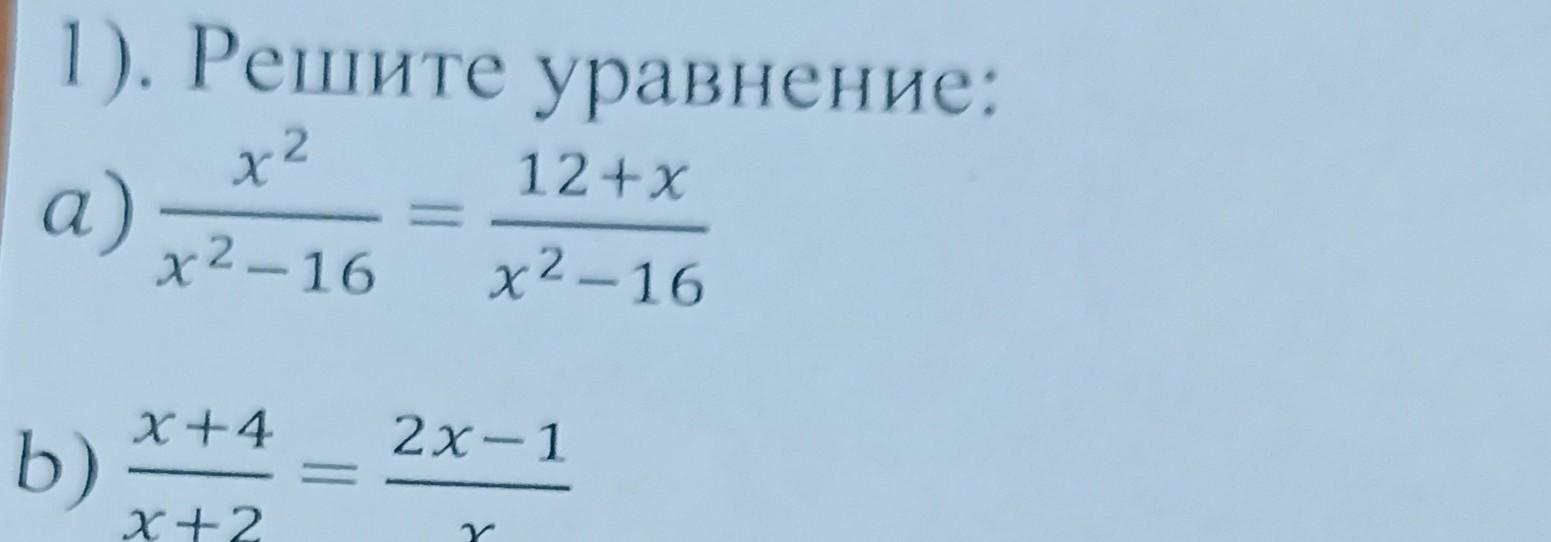
Ответы
а) х²/(х² - 16) = (12 + х)/(х² - 16)
одз: х² - 16 не равно 0 => х +-4 не равно 0
х²(х²-16) = (12 + х)(х² - 16) (крест накрест умножение)
х²(х² - 16) - (12 + х)(х² - 16) = 0
(х² - 16)(х² - х - 12) = 0
х² - 16 = 0 или х² - х - 12
х² - 16 не равно 0 по одз, тогда
х² - х - 12 = 0
D = 1 + 12×4 = 49 = 7²
х1 = (1 + 7)/2 = 4; х2 = (1 - 7)/2 = -3
х1 не подходит по одз
Ответ: -3
б) (х+4)/(х+2) = (2х - 1)/х
одз: х + 2 не равно 0 => х не равно - 2
х не равно 0
х(х + 4) = (х + 2)(2х - 1) (крест накрест умножение)
х² + 4х = 2х² - 2 + 3х
х² - х - 2 = 0
D = 1 + 4×2 = 9 = 3²
х1 = (1+3)/2 = 2; х2 = (1-3)/2 = -1
Ответ: 2; -1
Переносим всё в левую часть с противоположным знаком.
х²/(х²-16) - (12+х)/(х²-16) = 0
в этом уравнении x²-16 != 0, т.к. знаменатель не равен нулю. х != 4; -4
Домножаем всё выражение на знаменатель (не забываем про ограничения)
х² - (12+х) = 0
х² - х - 12 =0
По сколько дискриминант больше нуля (1² - (-12*1*4) = 49 ), то уравнение имеет два корня.
Далее мы можем воспользоваться теоремой Виета.
х1 + х2 = 1
х1*х2 = -12
х1 = -3
х2= 4, не удовлетворяет ограничениям (см. начало)
Ответ: -3