Предмет: Алгебра,
автор: BrawllStarss
Найти значение суммы
Приложения:
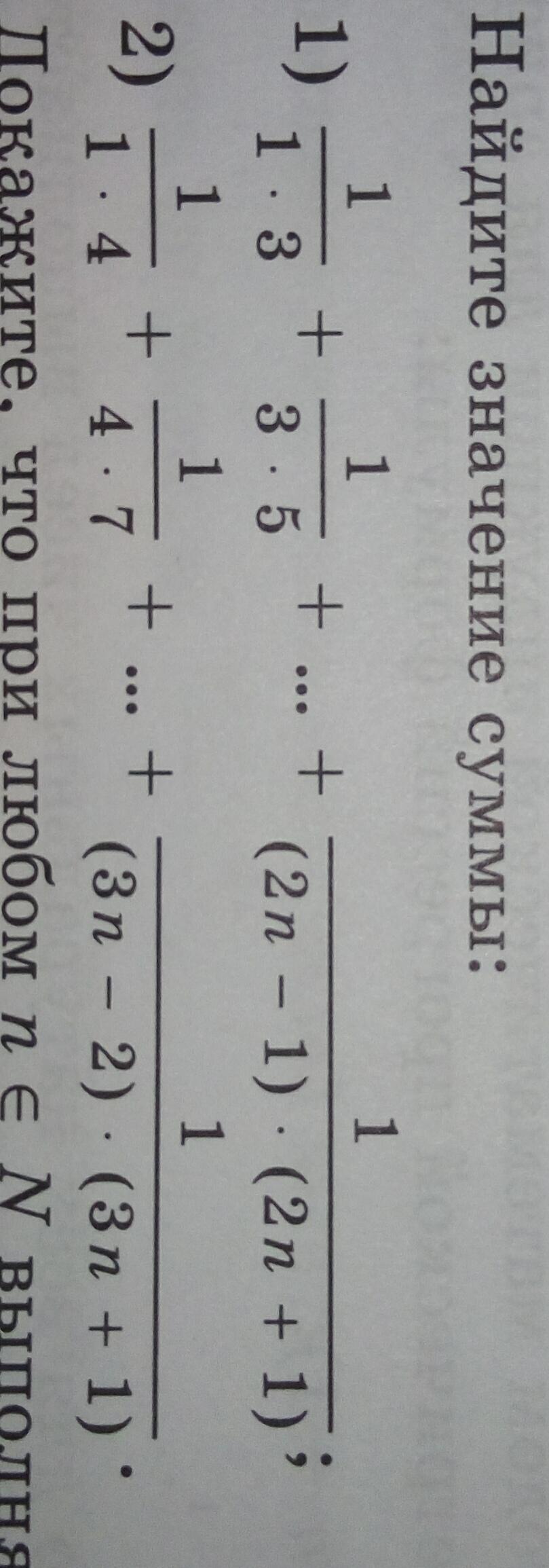
Ответы
Автор ответа:
3
⇒
⇒
⇒
⇒
⇒
⇒
Получаем
2)
Аналогично
Автор ответа:
4
Ответ:
Для нахождения коэффициентов при разложении правильной дроби на сумму простейших дробей пользуемся методом неопределённых коэффициентов .
Похожие вопросы
Предмет: Русский язык,
автор: яхино
Предмет: Русский язык,
автор: zhukovaesya
Предмет: Русский язык,
автор: mintyan
Предмет: Биология,
автор: abcdefghleon