Демо задание 1-3
Номер 2

Ответы
Ответ:
1) Уравнение плоскости ABC, проходящей через три точки имеет вид:
Пусть первая точка - точка А, вторая - В , третья - С .
Уравнение пл. АВС : .
Для удобства построения плоскости запишем это уравнение как уравнение плоскости в отрезках , где a , b , c - отрезки, отсекаемые плоскостью на соответствующих осях координат . Абсолютные величины чисел a, b и c равны длинам отрезков, которые плоскость отсекает на координатных осях OХ, OУ и OZ соответственно, считая от начала координат. Знак чисел a, b и c показывает, в каком направлении (положительном или отрицательном) откладываются отрезки на координатных осях.
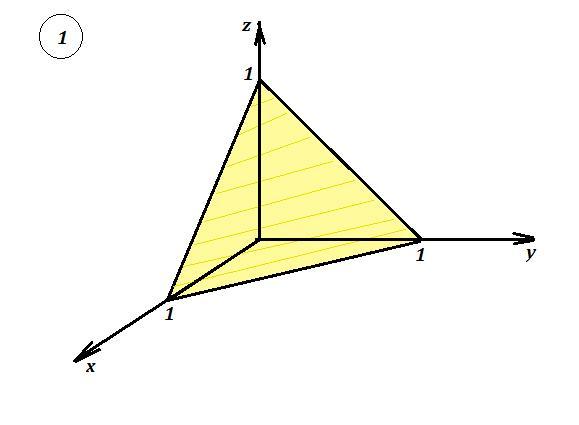
На осях ОХ , ОУ , OZ плоскость отсекает отрезки , равные 1 . Плоскость схематически построена на рис.1 .
2) Уравнение прямой АВ .
Найдём координаты направляющего вектора ВА :
Канонические уравнения прямой АВ : .
Запишем уравнение прямой АВ в параметрическом виде :
Запишем уравнение прямой АВ как пересечение двух плоскостей:
.
3) Длина высоты h , проведённой из вершины О на пл. АВС .
Найдём сначала площадь плоскости АВС : .
Найдём объём тетраэдра по формуле: .
Так как объём пирамиды равен , то
.