Предмет: Алгебра,
автор: eleonaise
Демо задание 1-3
Номер 3
Приложения:

Simba2017:
не видно
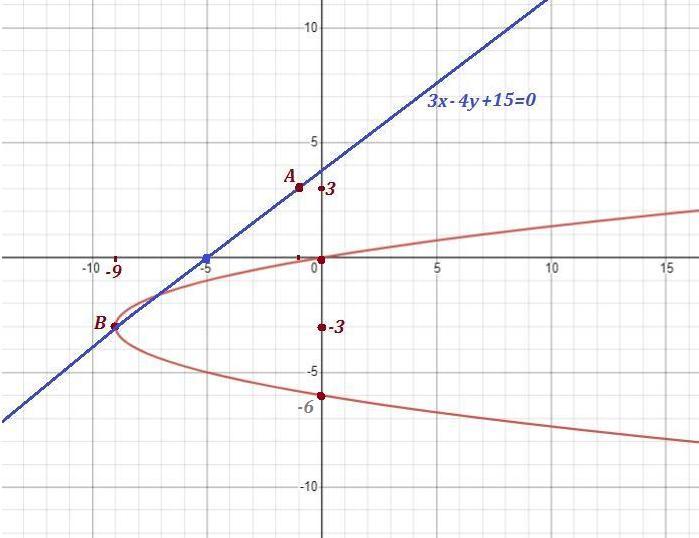
A (-1; 3) уравнение y^2+6y=x
вершину параболы найти не можете?
(-9;-3)
Тут задают вопросы чтобы их кто-то решил. Конкретно мне нужно чье-то решение (вариант из решений) для демо задания.
я ответов не пишу
Я и не просила :)
Ответы
Автор ответа:
1
Ответ:
Это каноническое уравнение пaраболы. Вершина параболы находится в точке B( -9 , -3 ) , ветви направлены вправо .
Канонические уравнения прямой, проходящей через точки
А( -1 , 3 ) и В( -9 , -3 ) .
По свойству пропорции .
Это общее уравнение прямой .
Параметрические уравнения : .
Приложения:
Похожие вопросы
Предмет: Русский язык,
автор: АняКонник16
Предмет: Русский язык,
автор: александра415
Предмет: Русский язык,
автор: АняКонник16
Предмет: Математика,
автор: samedismailoxwyrw