Предмет: Алгебра,
автор: rootправа
Решить неравенство.
14 задание ЕГЭ
Приложения:
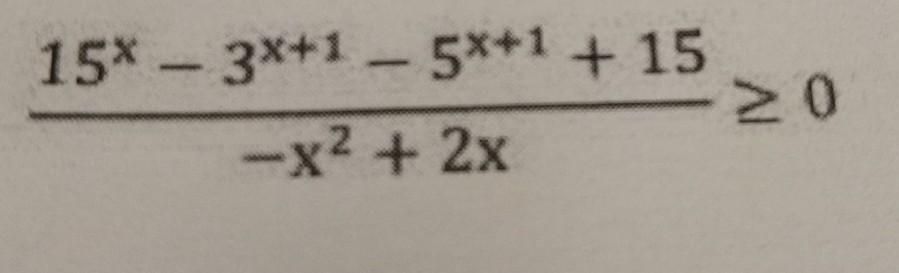
Ответы
Автор ответа:
1
Ответ:
Объяснение:
rootправа:
хотел 5 поставить, но промахнулся (
спасибо за помощь !
Похожие вопросы
Предмет: Английский язык,
автор: Аноним
Предмет: Українська мова,
автор: сашка290
Предмет: Українська мова,
автор: валюша301
Предмет: Английский язык,
автор: llavepizza
Предмет: Математика,
автор: sumayabegim