Предмет: Алгебра,
автор: widownes
Решите производную функции
Приложения:
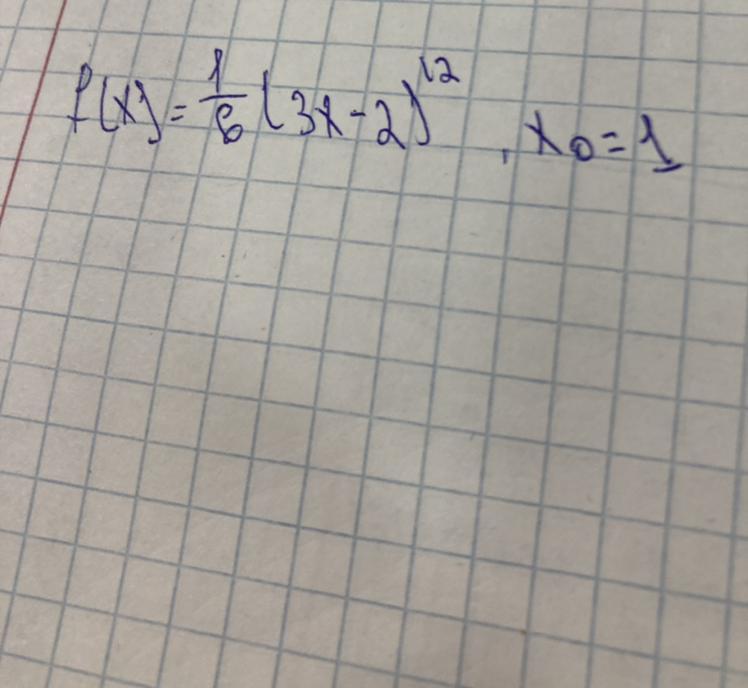
Ответы
Автор ответа:
1
Ответ:
Автор ответа:
1
Ответ:
Объяснение:
Функция:
f(x) = (1/6)·(3x - 2)¹²
Производная функции:
f'(x) = (1/6)·12· (3x - 2)¹¹ · 3 = 6·(3x - 2)¹¹
f'(1) = 6·(3·1 - 2)¹¹ = 6
matig3361:
DedStar помогите пожалуйста с моим заданием!
Похожие вопросы
Предмет: Черчение,
автор: erkenova0909
Предмет: Английский язык,
автор: Martina17
Предмет: Английский язык,
автор: Tsyganova20031
Предмет: Русский язык,
автор: NeonIgor