Предмет: Алгебра,
автор: Аноним
Розвязать уравнение
8 класс алгебра
Приложения:
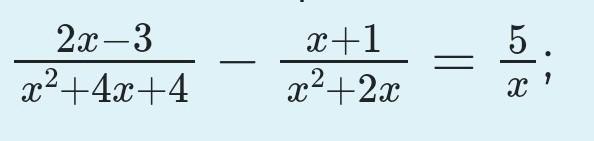
Ответы
Автор ответа:
2
Ответ:
х=(-1) и х=(-5.5)
Решение:
Формула сокращённого умножения:
По этой формуле х²+4х+4 мы можем записать как (х+2)². Также вынесем х в знаменателе второй дроби.
Приведём дроби к общему знаменателю:
Если дробь равна нулю, числитель равен нулю, знаменатель - не равен нулю.
ОДЗ:
х(х+2)² ≠ 0
х≠0 и (х+2)²≠0
х≠0 и х+2≠0
х≠0 и х≠(-2)
Прировняем числитель дроби к нулю:
Приведём подобные слагаемые:
Умножим уравнение на (-1):
Имеем квадратное уравнение. Решим по дискриминанту.
Учёв ОДЗ, имеем два решения: х=(-1) и х=(-5.5).
Fire1ce:
Спасибо, мне приятно, рад помочь)
Похожие вопросы
Предмет: Окружающий мир,
автор: окси126
Предмет: Английский язык,
автор: kaysom
Предмет: Русский язык,
автор: ДЖГРД
Предмет: Информатика,
автор: Аноним
Предмет: История,
автор: skymasterskymaster23