Предмет: Алгебра,
автор: spamgg002
нужно РЕШИТЬ показательные неравенства ЕГЭ все расписать (желательно с пояснениями) , если не знаете не пиши ....
Приложения:
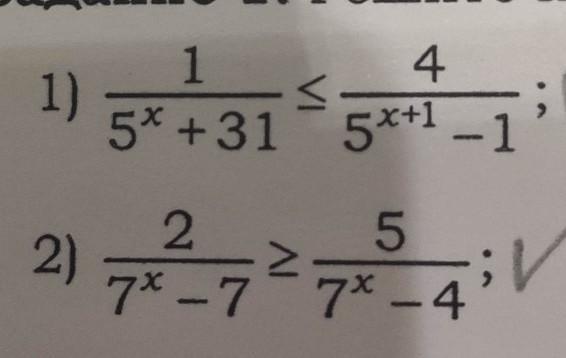
Ответы
Автор ответа:
0
Объяснение:
1) ОДЗ: 5ˣ⁺¹-1≠0 5ˣ⁺¹≠1 5ˣ⁺¹≠5⁰ х+1≠0 х≠-1.
-∞__-__-1__+__3__-__+∞
Ответ: x∈(-1;3].
2) ОДЗ: 7ˣ-7≠0 7ˣ≠7¹ x≠1 7ˣ-4≠0 7ˣ≠4 log₇7ˣ≠log₇4 x≠log₇4.
-∞__-__log₇4__+__1__-__log₇9__+__+∞
Ответ: x∈(-∞;log₇4)U(1;log₇9].
Я решаю 2).
хорошо.....
сколько ждать ....?
Похожие вопросы
Предмет: Русский язык,
автор: yuliyarevenko
Предмет: Английский язык,
автор: remyfoxxx
Предмет: Английский язык,
автор: Xomeg
Предмет: Русский язык,
автор: Lera20186
Предмет: Русский язык,
автор: 1023911sz
и привести к общему знаменателю
и метод интервалов