Предмет: Геометрия,
автор: MuradTaimov
Точки A,B,C,D,E последовательно расположены на прямой b, причем CD=1 и AB=BC=DE=2. Окружности v и w, касающиеся друг друга, таковы, что v проходит через точки D и E, ф w-через точки B и С. Найти радиусы этих окружностей, если известно, что их центры и точка A на одной прямой.
orjabinina:
а может чертеж был?
Не был
Я не могу ее решить трудная :(
11/2√19 и 8/√19
Ответы
Автор ответа:
6
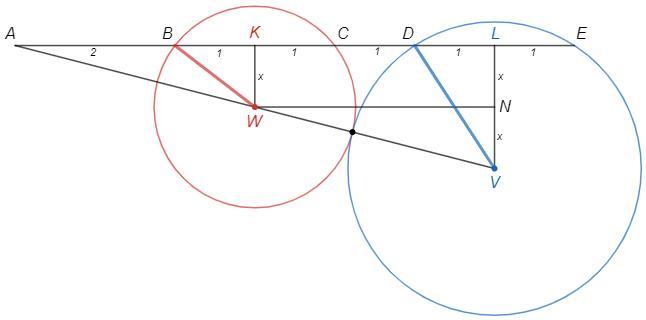
W, V - центры
Проведем WK⊥AE, VL⊥AE
BK=1, DL=1 (перпендикуляр из центра к хорде делит ее пополам)
AK=3, AL=6
Проведем WN⊥VL
Понятно, что W - середина AV, N - середина VL
WK=VN=NL=x
Rw =WB =√(WK^2+BK^2) =√(x^2+1)
Rv =VD =√(VL^2+DL^2) =√(4x^2+1)
WV =Rw+Rv (точка касания лежит на линии центров)
WV =√(VN^2+WN^2) => Rw+Rv =√(x^2+9)
√(x^2+1) + √(4x^2+1) = √(x^2+9)
x^2 +1 +4x^2 +1 +2√(x^2+1)√(4x^2+1) = x^2 +9
4(x^2+1)(4x^2+1) = (7-4x^2)^2 // при 7-4x^2 >=0 => x<=√7/2
16x^4 +16x^2 +4x^2 +4 = 49 -56x^2 +16x^4
76x^2 = 45 => x=√(45/76)
Rw =√(45/76 +1) =√(121/76) =11/2√19
Rv =√(4*45/76 +1) =√(256/76) =8/√19
Приложения:
Спасибо , siestarjoki. Интересно, а внутреннее касание может быть.
да, с другими числами. Тогда расстояние между центрами будет разностью радиусов
Похожие вопросы
Предмет: Русский язык,
автор: салохидин
Предмет: Русский язык,
автор: машарипов
Предмет: Русский язык,
автор: Lade1
Предмет: Русский язык,
автор: aliya6580
Предмет: Математика,
автор: Atlqh