Предмет: Алгебра,
автор: AntonAntonov
Как решать? Логарифмическое уравнение
Приложения:
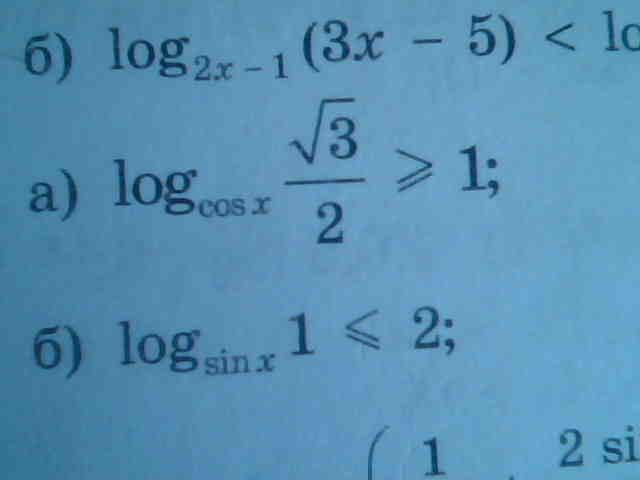
Ответы
Автор ответа:
0
Видны только вторая и третья строчка, поэтому вот:
а) log(cosx)(√3/2) ≥ 1
1 = log(cosx)(cosx) = логарифм по основанию cosx от cosx
ОДЗ: 0 < cosx < 1, -π/2 + 2πk < x < π/2 + 2πk
√3/2 ≤ cosx,
cosx ≥ √3/2
-π/6 + 2πk ≤ x ≤ π/6 + 2πk - удовлетворяет ОДЗ
б) log(sinx)(1) < 2
ОДЗ: 0 < sinx < 1; 2πk < x < π + 2πk
1 > sin^2(x)
sin^2(x) < 1
0 < sinx < 1
2πk < x < π + 2πk - удовлетворяет ОДЗ
а) log(cosx)(√3/2) ≥ 1
1 = log(cosx)(cosx) = логарифм по основанию cosx от cosx
ОДЗ: 0 < cosx < 1, -π/2 + 2πk < x < π/2 + 2πk
√3/2 ≤ cosx,
cosx ≥ √3/2
-π/6 + 2πk ≤ x ≤ π/6 + 2πk - удовлетворяет ОДЗ
б) log(sinx)(1) < 2
ОДЗ: 0 < sinx < 1; 2πk < x < π + 2πk
1 > sin^2(x)
sin^2(x) < 1
0 < sinx < 1
2πk < x < π + 2πk - удовлетворяет ОДЗ
Похожие вопросы
Предмет: Математика,
автор: lollipopman
Предмет: История,
автор: anavakarina0
Предмет: Математика,
автор: robin228666
Предмет: Алгебра,
автор: fido97
Предмет: Алгебра,
автор: Vanilka20